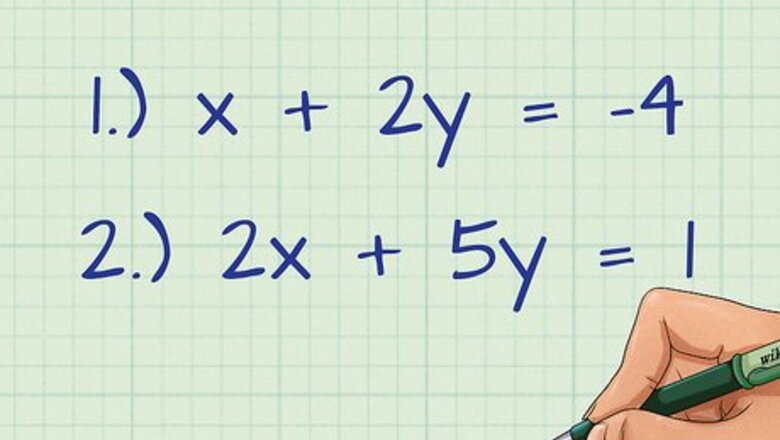
views
X
Research source
While it involves several steps, the substitution method for solving simultaneous equations requires only basic algebra skills.
Finding the Value of y
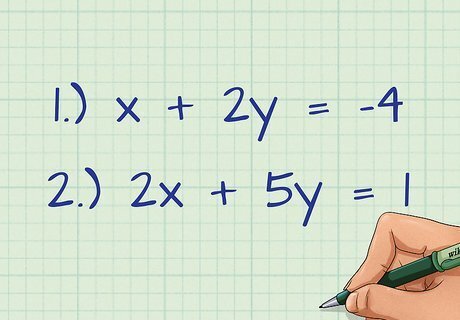
Choose the equation you want to work with first. It doesn’t matter which equation you choose, but you might want to look for one that will give you numbers that are easier to work with. For example, if your simultaneous equations are 1) x + 2 y = − 4 {\displaystyle x+2y=-4} x+2y=-4 and 2) 2 x + 5 y = 1 {\displaystyle 2x+5y=1} 2x+5y=1, you will probably want to begin with the first equation, because the x {\displaystyle x} x is already by itself.
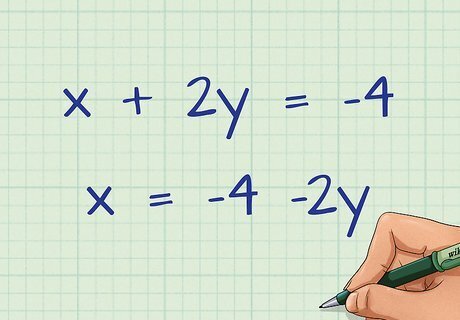
Isolate the x {\displaystyle x} x variable in the first equation. You could also start by isolating the y variable (or whatever other variable the equation uses). For example, if you are beginning with x + 2 y = − 4 {\displaystyle x+2y=-4} x+2y=-4, you could solve for x {\displaystyle x} x by subtracting 2y from each side. x + 2 y = − 4 {\displaystyle x+2y=-4} x+2y=-4 x = − 4 − 2 y {\displaystyle x=-4-2y} x=-4-2y
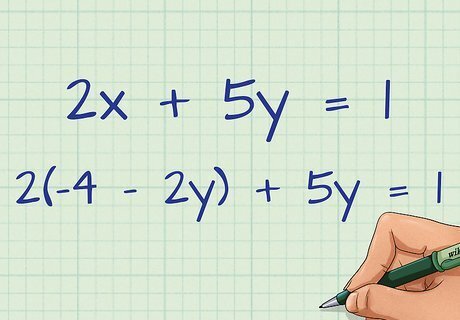
Plug in the value of x {\displaystyle x} x into the second equation. Place the value in parentheses for clarity. For example, if you found x = − 4 − 2 y {\displaystyle x=-4-2y} x=-4-2y in the first equation, plug in − 4 − 2 y {\displaystyle -4-2y} -4-2y for x {\displaystyle x} x in the second equation: 2 x + 5 y = 1 {\displaystyle 2x+5y=1} 2x+5y=1 2 ( − 4 − 2 y ) + 5 y = 1 {\displaystyle 2(-4-2y)+5y=1} 2(-4-2y)+5y=1
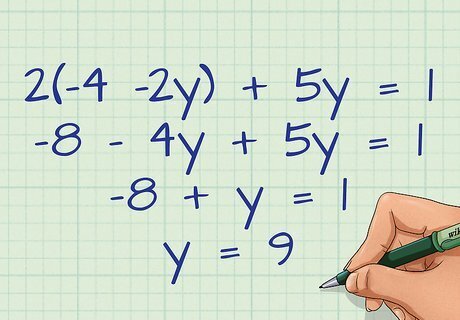
Find the value of y {\displaystyle y} y in the second equation. Remember to follow the order of operations. For example, to solve for y {\displaystyle y} y in the equation 2 ( − 4 − 2 y ) + 5 = 1 {\displaystyle 2(-4-2y)+5=1} 2(-4-2y)+5=1, first use the distributive property to multiply. 2 ( − 4 − 2 y ) + 5 y = 1 {\displaystyle 2(-4-2y)+5y=1} 2(-4-2y)+5y=1 − 8 − 4 y + 5 y = 1 {\displaystyle -8-4y+5y=1} -8-4y+5y=1 − 8 + y = 1 {\displaystyle -8+y=1} -8+y=1 y = 9 {\displaystyle y=9} y=9
Finding the Value of x
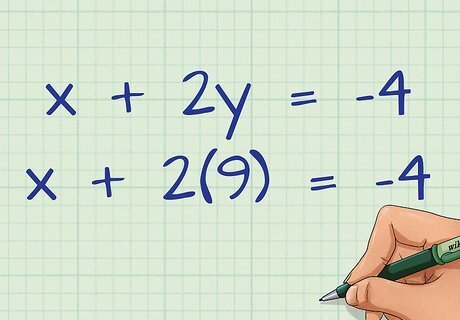
Plug in the y {\displaystyle y} y value into either equation. It doesn’t matter which equation you use, as long as you use the original equation, or an equation where you’ve isolated the x {\displaystyle x} x variable. This will allow you to find the value for x {\displaystyle x} x. If you plug the y {\displaystyle y} y value back into the second equation with the x {\displaystyle x} x substitution, you will not be able to find the value of x {\displaystyle x} x. For example, if you found y = 9 {\displaystyle y=9} y=9, plug in 9 {\displaystyle 9} 9 for y {\displaystyle y} y in the first equation: x + 2 y = − 4 {\displaystyle x+2y=-4} x+2y=-4 x + 2 ( 9 ) = − 4 {\displaystyle x+2(9)=-4} x+2(9)=-4
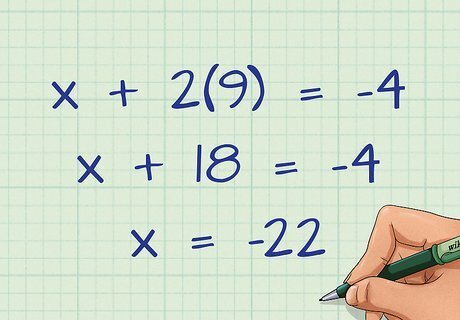
Find the value of x {\displaystyle x} x. Remember to follow the order of operations. For example, to solve for x {\displaystyle x} x in the equation x + 2 ( 9 ) = − 4 {\displaystyle x+2(9)=-4} x+2(9)=-4, first multiply, and then subtract 18 from each side to find the value of x {\displaystyle x} x. x + 2 ( 9 ) = − 4 {\displaystyle x+2(9)=-4} x+2(9)=-4 x + 18 = − 4 {\displaystyle x+18=-4} x+18=-4 x = − 22 {\displaystyle x=-22} x=-22.
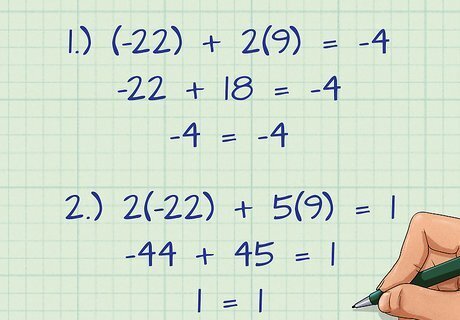
Check your work. To do this, substitute the values you found for x {\displaystyle x} x and y {\displaystyle y} y into both equations, and verify that the resulting equation are true. For example, if you found y = 9 {\displaystyle y=9} y=9 and x = − 22 {\displaystyle x=-22} x=-22, substitute these values into both equations. So, for the first equation: ( − 22 ) + 2 ( 9 ) = − 4 {\displaystyle (-22)+2(9)=-4} (-22)+2(9)=-4 − 22 + 18 = − 4 {\displaystyle -22+18=-4} -22+18=-4 − 4 = − 4 {\displaystyle -4=-4} -4=-4 For the second equation: 2 ( − 22 ) + 5 ( 9 ) = 1 {\displaystyle 2(-22)+5(9)=1} 2(-22)+5(9)=1 − 44 + 45 = 1 {\displaystyle -44+45=1} -44+45=1 1 = 1 {\displaystyle 1=1} 1=1

















Comments
0 comment