
views
Using Long Division

Determine the dividend and the divisor. The dividend is the number you are dividing, the divisor is the number you are dividing by. In this instance, the odd number will be the dividend, and the divisor will be 2. For example, if you are calculating 17 ÷ 2 {\displaystyle 17\div 2} 17\div 2, the dividend is 17, and the divisor is 2.

Place the dividend under a long division symbol. A long division symbol looks like the left and top side of a box. Place the divisor on the outside of the long division symbol, to the left of the box. For example: 2 ) 17 ¯ {\displaystyle 2{\overline {)17}}} 2{\overline {)17}}.
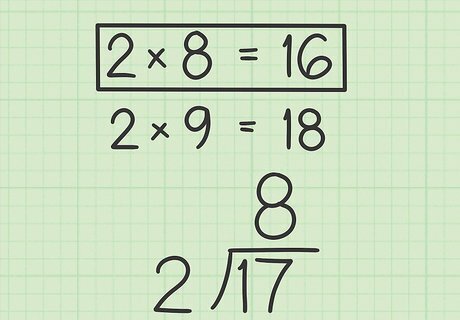
Divide the dividend by 2. Since you can’t divide an odd number by 2, you need to find the greatest number of times 2 will divide evenly into the dividend. Use the multiples of 2 to help you determine what this number is. Place this number on top of the division symbol. For example, the greatest number of times 2 can divide evenly into 17 is 8, since 2 × 8 = 16 {\displaystyle 2\times 8=16} 2\times 8=16. So you should place 8 on top of the long division symbol.
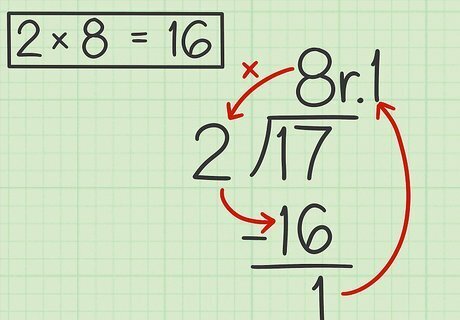
Multiply the number on top of the long division symbol by the divisor. Place this number below the dividend and subtract. The difference is your remainder. When you divide an odd number by 2, you will always have a remainder of 1. For example, 2 × 8 = 16 {\displaystyle 2\times 8=16} 2\times 8=16 and 17 − 16 = 1 {\displaystyle 17-16=1} 17-16=1, So 17 ÷ 2 = 8 r 1 {\displaystyle 17\div 2=8r1} 17\div 2=8r1.
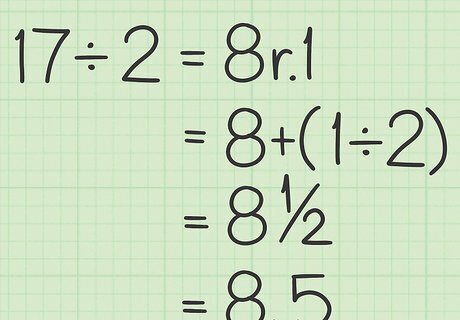
Convert the remainder to a fraction. To do this, change the remainder into the numerator of a fraction. The denominator of the fraction will be the divisor, in this case, 2. You can change this fraction to a decimal as well. The fraction 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} always converts to 0.5 {\displaystyle 0.5} 0.5. For example, 17 ÷ 2 = 8 r 1 {\displaystyle 17\div 2=8r1} 17\div 2=8r1.By turning the remainder into a fraction, you get 17 ÷ 2 = 8 1 2 {\displaystyle 17\div 2=8{\frac {1}{2}}} 17\div 2=8{\frac {1}{2}}.By turning the fraction into a decimal, you get 17 ÷ 2 = 8.5 {\displaystyle 17\div 2=8.5} 17\div 2=8.5
Breaking Up a Two-Digit Number
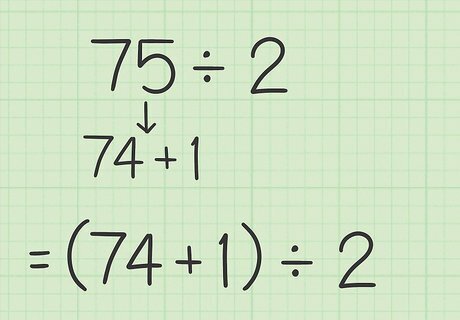
Turn the number you are dividing into an even number +1. An odd number will always have a remainder of 1 when dividing by 2. So breaking up the number in this way helps you divide the number quickly, since an even number will have no remainder when dividing by 2. To break up the number into an even number +1, subtract 1 from the number. For example, if you are calculating 75 ÷ 2 {\displaystyle 75\div 2} 75\div 2, break up 75 {\displaystyle 75} 75 into 74 + 1 {\displaystyle 74+1} 74+1.
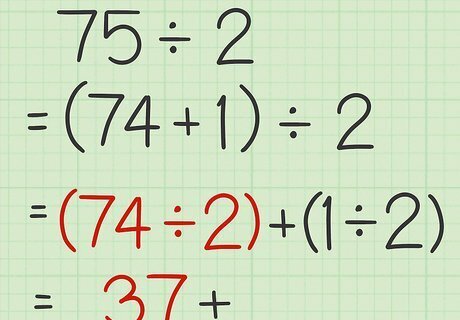
Divide the even number by 2. You will likely be able to do this in your head, since it will divide evenly. The easiest way to do it is to take half of the tens and half of the ones, then add them together. For example, half of 70 is 35, and half of 4 is 2, so 74 ÷ 2 = 35 + 2 = 37 {\displaystyle 74\div 2=35+2=37} 74\div 2=35+2=37.

Add 0.5 to the quotient. Since 1 ÷ 2 = 0.5 {\displaystyle 1\div 2=0.5} 1\div 2=0.5 to reach your final answer, you need to add the two parts together: the even number divided by 2, and 1 divided by 2. For example, 37 + 0.5 = 37.5 {\displaystyle 37+0.5=37.5} 37+0.5=37.5. So, 75 ÷ 2 = 37.5 {\displaystyle 75\div 2=37.5} 75\div 2=37.5.
Breaking Up a Three-Digit or Larger Number
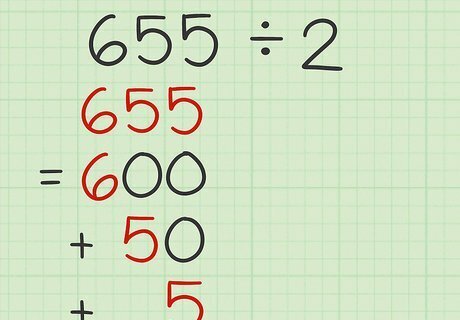
Write the number in expanded notation. Expanded notation is breaking up the number to show the value of each digit, according to its place value. For example, 655 = 600 + 50 + 5 {\displaystyle 655=600+50+5} 655=600+50+5.
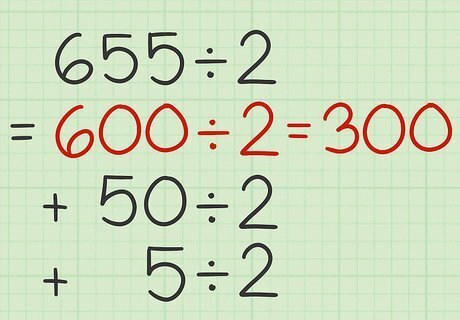
Divide the hundreds place by 2. Or, if you have a larger number, begin with the largest place value, such as thousands or ten thousands. You will likely be able to complete this division in your head. If not, you can calculate it quickly by hand. Since the number ends in 0, it is even and will be evenly divisible by 2. Set this quotient aside for now. For example, 600 ÷ 2 = 300 {\displaystyle 600\div 2=300} 600\div 2=300.
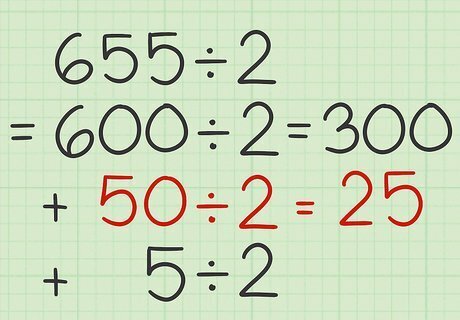
Divide the tens place by 2. You will likely be able to do this in your head, but you can also do it by hand if need be. Since the number is a multiple of 10 it will be evenly divisible by 2. Set this quotient aside for now. For example, 50 ÷ 2 = 25 {\displaystyle 50\div 2=25} 50\div 2=25.
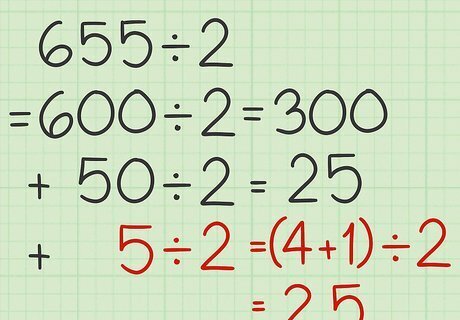
Break up the number in the ones place into an even number +1. Then, divide the even number by 2. You should have no remainder; the remainder is the +1 you removed when you broke up the number. For example, 5 = 4 + 1 {\displaystyle 5=4+1} 5=4+1. Now, dividing the even number, you should calculate 4 ÷ 2 = 2 {\displaystyle 4\div 2=2} 4\div 2=2.
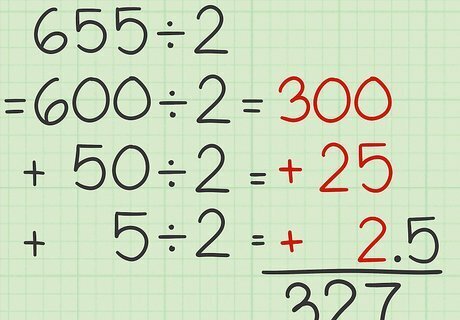
Add the quotients for all the place values. Since you expanded the number into place values, and divided each place value individually by 2, now you have to add them back together again. For example, 300 + 25 + 2 = 327 {\displaystyle 300+25+2=327} 300+25+2=327.
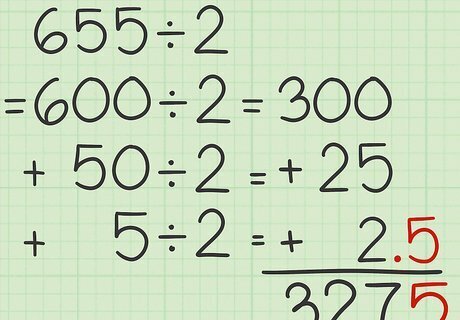
Add 0.5 to the sum. Since you removed the remainder of 1 from the ones place before dividing by 2, you now have to take half of that 1 and add it back into your final answer. For example, 327 + 0.5 = 327.5 {\displaystyle 327+0.5=327.5} 327+0.5=327.5.



















Comments
0 comment