How to Determine Whether Two Variables Are Directly Proportional

Rewriting the Equation of the Line

Understand direct proportion. Two variables are in direct proportion if each variable changes at the same rate. In other words, if x {\displaystyle x} x changes by a certain factor or constant ( k {\displaystyle k} k), then y {\displaystyle y} y changes by that same constant ( k {\displaystyle k} k).

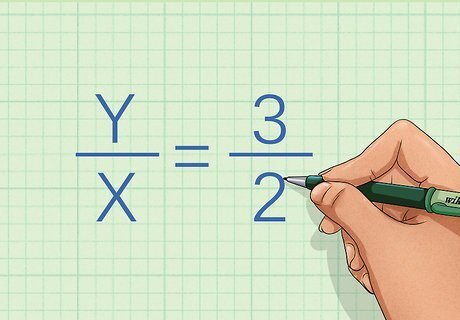
Write down the equation of the line. The equation will have two variables and a constant. If you are not given the equation, you cannot use this method. For example, you might be given the equation y x = 3 2 {\displaystyle {\frac {y}{x}}={\frac {3}{2}}} {\frac {y}{x}}={\frac {3}{2}}.

Rewrite the equation in the form of direct proportion, or variation. The equation is y = k x {\displaystyle y=kx} y=kx, where y {\displaystyle y} y equals the y-coordinate of a point on the line, x {\displaystyle x} x equals the x-coordinate for that same point, and k {\displaystyle k} k is the constant, or slope of the line. Use algebra to rearrange the equation in the form of y = k x {\displaystyle y=kx} y=kx. If you can’t rewrite the equation in this form, the variables are not directly proportional. If you can, it proves that they are directly proportional. For example, if you multiply both sides of the equation y x = 3 2 {\displaystyle {\frac {y}{x}}={\frac {3}{2}}} {\frac {y}{x}}={\frac {3}{2}} by x {\displaystyle x} x, the equation becomes y = 3 2 x {\displaystyle y={\frac {3}{2}}x} y={\frac {3}{2}}x, which is in the form of y = k x {\displaystyle y=kx} y=kx, with 3 2 {\displaystyle {\frac {3}{2}}} {\frac {3}{2}} being the constant.

Using a Set of Points

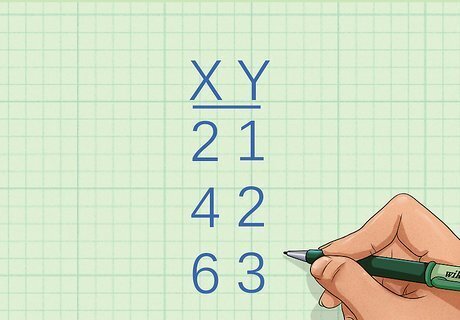
Identify the x-coordinates of the first two points. You should be given a list of coordinates, or have a graph from which you can determine the coordinates of the points. If you don’t have the coordinates of points on the line, you cannot use this method. For example, you might be given the set of points x y 2 1 4 2 6 3 {\displaystyle {\begin{matrix}x&y\\\hline \\2&1\\4&2\\6&3\end{matrix}}} {\begin{matrix}x&y\\\hline \\2&1\\4&2\\6&3\end{matrix}} The x-coordinate of the first point is 2, and the x-coordinate of the second point is 4.

Determine the factor by which the x {\displaystyle x} x variable grows. To do this, determine which factor, or constant, the first x-coordinate is multiplied by to arrive at the second coordinate. For example, if the first x-coordinate is 2, and the second x-coordinate is 4, you need to determine what you multiply 2 by to get 4: 2 k = 4 {\displaystyle 2k=4} 2k=4 2 k 2 = 4 2 {\displaystyle {\frac {2k}{2}}={\frac {4}{2}}} {\frac {2k}{2}}={\frac {4}{2}} k = 2 {\displaystyle k=2} k=2So, the x {\displaystyle x} x variable grows by the constant 2.

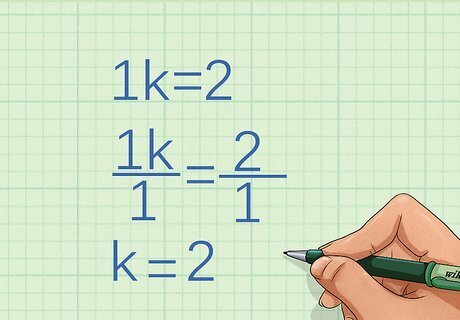
Determine the factor by which the y {\displaystyle y} y variable grows. Use the same two points you used to determine the growth of x {\displaystyle x} x. Use algebra to determine the factor by which the two coordinates vary. For example, if the first y-coordinate is 1, and the second y-coordinate is 2, you need to determine what you multiply 1 by to get 2: 1 k = 2 {\displaystyle 1k=2} 1k=2 1 k 1 = 2 1 {\displaystyle {\frac {1k}{1}}={\frac {2}{1}}} {\frac {1k}{1}}={\frac {2}{1}} k = 2 {\displaystyle k=2} k=2So, the variable y {\displaystyle y} y grows by the constant 2.

Compare the constants of the two variables. If x {\displaystyle x} x and y {\displaystyle y} y changed at the same rate, or by the same factor, then they are directly proportional. For example, since the x-coordinates changed by a factor of 2 while the y-coordinates also changed by a factor of 2, the two variables are directly proportional.

Using a Graph

Note whether the line is straight. When two variables are in proportion, the line representing them will be straight. This means that the slope of the line is constant, or follows the equation y = k x {\displaystyle y=kx} y=kx.

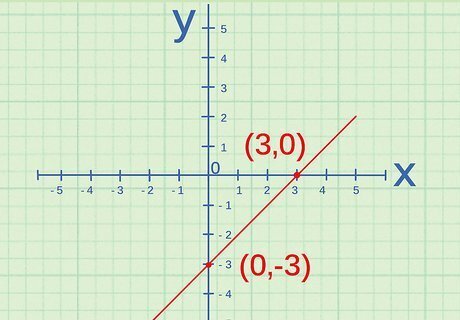
Determine the y-intercept. The y-intercept is the point where the line crosses the y-axis. When two variables are directly proportional, when graphed their line will cross through the origin. The origin is at the point ( 0 , 0 ) {\displaystyle (0,0)} (0,0), so the y-intercept of the line should be 0 {\displaystyle 0} {\displaystyle 0}. If it isn’t, the variables are not directly proportional. The y-axis is the vertical axis.

Find the coordinates of two points on the line. Compare the coordinates with each other, and determine whether each coordinate changed by the same factor. That is, determine whether the constant ( k {\displaystyle k} k) is the same for both the x {\displaystyle x} x and y {\displaystyle y} y values. For example, if the first point is ( 1 , 3 ) {\displaystyle (1,3)} (1,3), and the second point is ( 2 , 6 ) {\displaystyle (2,6)} (2,6), the x-coordinate changed by a factor of 2, since 1 ( 2 ) = 2 {\displaystyle 1(2)=2} 1(2)=2. The y-coordinate also changed by a factor of 2, since 3 ( 2 ) = 6 {\displaystyle 3(2)=6} 3(2)=6. Thus, you can confirm that the line represents two variables that are directly proportional.

Completing Sample Problems

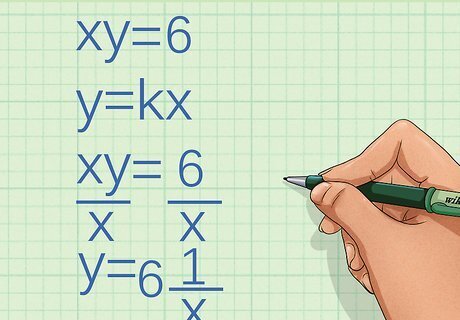
Look at the equation. Determine whether the two variables are directly proportional: x y = 6 {\displaystyle xy=6} xy=6. Remember that if the variables are directly proportional, they will follow the pattern y = k x {\displaystyle y=kx} y=kx. Use algebra to rewrite the equation. Isolate the y {\displaystyle y} y variable by dividing each side by x {\displaystyle x} x: x y x = 6 x {\displaystyle {\frac {xy}{x}}={\frac {6}{x}}} {\frac {xy}{x}}={\frac {6}{x}} y = 6 1 x {\displaystyle y=6{\frac {1}{x}}} y=6{\frac {1}{x}} Assess whether the rewritten equation follows the pattern y = k x {\displaystyle y=kx} y=kx. In this instance, the equation does not, so the variables are not directly proportional. In fact, they are inversely proportional.

Consider the following set of points. Are the variables directly proportional? x y 1 3 3 9 9 27 {\displaystyle {\begin{matrix}x&y\\\hline \\1&3\\3&9\\9&27\end{matrix}}} {\begin{matrix}x&y\\\hline \\1&3\\3&9\\9&27\end{matrix}} Determine the growth of x {\displaystyle x} x. Do this by finding the factor you multiply the first x-coordinate by to reach the second coordinate: 1 k = 3 {\displaystyle 1k=3} 1k=3 1 k 1 = 3 1 {\displaystyle {\frac {1k}{1}}={\frac {3}{1}}} {\frac {1k}{1}}={\frac {3}{1}} k = 3 {\displaystyle k=3} k=3So, the x-coordinate grows by factor of 3. Determine the growth of y {\displaystyle y} y: 3 k = 9 {\displaystyle 3k=9} 3k=9 3 k 3 = 9 3 {\displaystyle {\frac {3k}{3}}={\frac {9}{3}}} {\frac {3k}{3}}={\frac {9}{3}} k = 3 {\displaystyle k=3} k=3So, the y-coordinate grows by factor of 3. Compare the factor, or constant, of the two variables. They both grow by a factor of 3. Therefore, the variables are directly proportional.

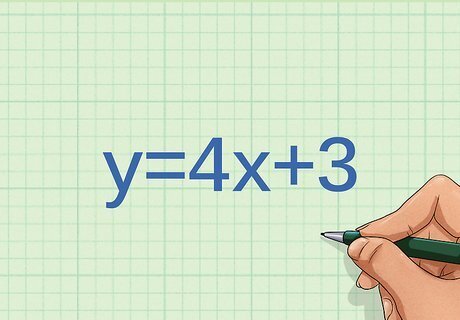
Consider a graph of the line y = 4 x + 3 {\displaystyle y=4x+3} y=4x+3. Does the graph show direct proportion between variables? Note whether the line is straight. Since the equation of the line is in slope-intercept form, it has a constant slope, meaning the line is straight. So potentially, the variables are directly proportional. Determine the y-intercept. If the variables are directly proportional, the line will pass through the point ( 0 , 0 ) {\displaystyle (0,0)} (0,0). The y-intercept of this line is the point ( 0 , 3 ) {\displaystyle (0,3)} (0,3). So, the variables are not directly proportional.