How to Check if a Function Is Continuous: Precalculus Review

UrbanPulse

Editor

posted on 2 years ago — updated on 1 second ago

21
views

Checking the continuity of a function is easy! The simple rule for checking is tracing your pen on the curve. If you have to pick up your pen, the function is discontinuous. We’ll review types of discontinuity and how to use limits to identify continuity at a point or over an interval. This wikiHow guide shows you how to check if a function is continuous.

Things You Should Know

This tutorial uses a general rule (tracing) and limits to check for continuity.
Look for point, jump, and asymptotic discontinuities in your function.
For a point, take the limit of f(x) = f(c) for x approaches c.
For a closed interval, you’ll need to take two limits, one for each end of the interval.

Check for Discontinuity

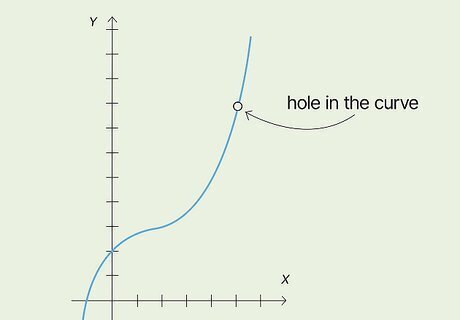
Look for a point discontinuity. This is also called a removable discontinuity. Discontinuities indicate that your function is not continuous. Point discontinuities occur when a point on a curve differs from the typical path of the function. You’ll see a hole in the curve where the point discontinuity is. This usually looks like an unfilled circle. The point will be somewhere above or below the hole. For example, if you have the function f(x) = x, you expect a straight, diagonal line crossing through the origin. However, if there’s a hole in the curve at x = 3, and a point at (3, 10), the function is discontinuous.

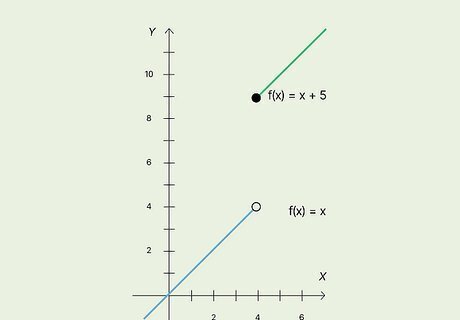
Check for a jump discontinuity. This is when the curve suddenly jumps to another disconnected curve. For example, for f(x) = x, let’s say at x = 4, the f(x) = x curve ends with a hole. Then, at x = 4, a second curve of f(x) = x + 5 begins. This second line is disconnected and above the first line.

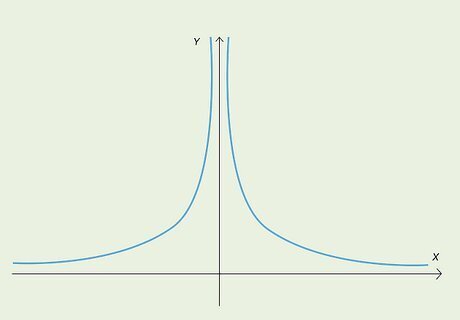
Identify an asymptotic discontinuity. These discontinuous functions have an asymptote that causes the parts of the function to tend toward an x value without reaching it.

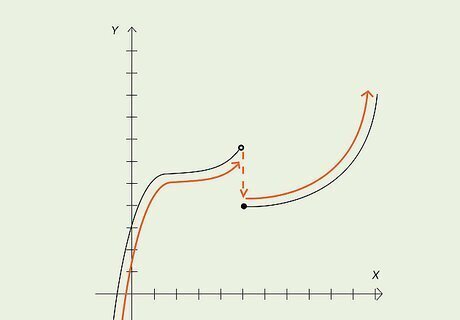
Trace the curve left to right. As a general rule, a function is discontinuous if you need to pick up your pencil as you trace the curve. The next section will cover how to check continuity using limits.

Checking over an Interval

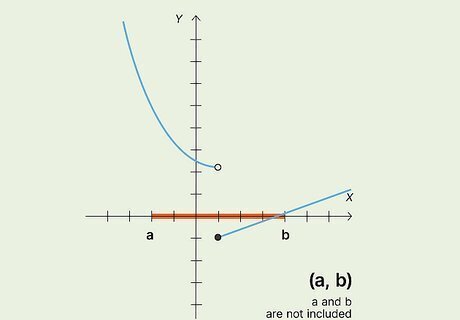
Trace the curve f(x) from a to b. For an open interval (a, b), check for discontinuity by tracing along the curve, not including a and b. If you needed to pick up your pen during the trace (e.g. for a point discontinuity), the curve is not continuous over the interval.

Check the limits for a and b. For a closed interval [a, b] you’ll need to check two limits. This is to check for holes (discontinuity) at either end of the curve. Take the limit of f(x) = f(a) for x approaches a+ (a from the right). Take the limit of f(x) = f(b) from x approaches b- (b from the left).