
views
Defining Car Loan Terms

Understand the amount you are borrowing. The amount you borrow is referred to as the principal amount. Your principal amount has several components. The formula for the principal amount of your car loan is (Purchase price) – (rebates) – (cash down payment) – (trade in value). A car purchase will also include fees and sales tax. Those two amounts are typically included in the principal amount. A rebate is a fixed amount of money paid to the buyer for the purchase of a particular vehicle. Rebates serve as an incentive to make the purchase. In most cases, the purchaser uses the rebate to reduce the principal amount of the loan. A cash down payment is paid by the purchaser. You may also trade in a vehicle- usually the car you are replacing. A trade in is something you sell as partial payment for something new. In this case, the value of the car you trade in reduces the purchase price on the new vehicle. Assume you’re buying a car for $20,000. The manufacturer provides a $2,000 rebate. You pay $3,000 as a down payment, and trade in a car valued at $5,000. The principal amount of your loan is $20,000 - $2,000 - $3,000 - $5,000, or $10,000.
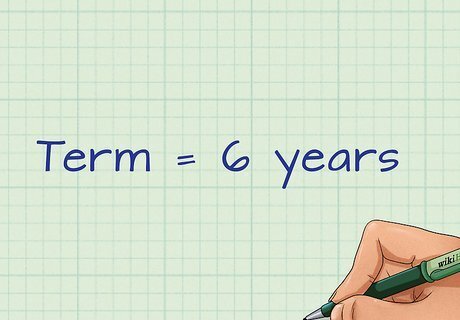
Determine the term of your loan. The loan term is the period of time that the loan will be outstanding. Most new car loans have a term of six years. The longer the term, the more interest you will pay on the principal balance.
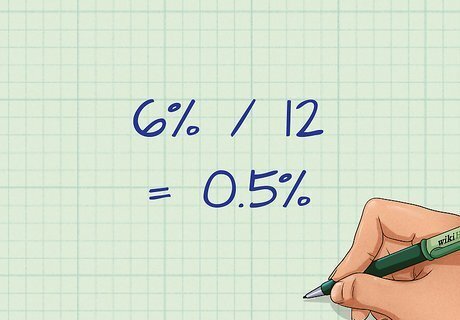
Compute the interest owed on the loan. The interest rate will be stated in your loan agreement. For car loans, the interest rate is commonly referred to as the Annual Percentage Rate, or APR. Your interest rate multiplied by the outstanding principal amount is the interest you owe for a particular period of time. Assume that your principal amount is $10,000. Your annual interest rate is 6%. You want to calculate the interest you owe for the month. Your interest rate for one month, also known as your monthly interest rate, is (6%/12 = 0.5%).
Computing Your Total Interest Using an Online Calculator
Use an amortization calculator. The formula for amortizing a loan is complex. The math required is difficult to perform manually. When a loan is amortized, the borrower makes a fixed loan payment, usually monthly. That payment includes both repayment of principal and interest owed on the debt. As time goes on, each fixed loan payment includes a larger portion of principal repayment, and a smaller portion of interest. There are many amortization calculators on the Internet allow you to input a principal amount, loan term and interest rate. The calculator can provide the monthly payment, based on the criteria you input. Try searching online for "car loan calculator" to find one.
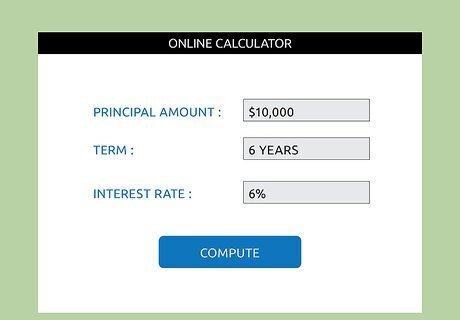
Input your assumptions. Assume that your loan’s principal amount is $10,000. The term of your loan is 6 years, and the interest rate on your loan is 6%. Input those amounts into the loan calculator.

Consider the amortization schedule that is produced. The schedule produces a monthly payment amount of $163.74. That schedule includes $50 of interest in the first monthly payment. The interest portion of each payment declines over time. For example, the interest portion in the 24th month’s payment is $35.93.

Find your total interest on the loan. The amortization schedule calculates total interest owed of $1932.48 over the life of the loan. If you want to reduce the total interest, you can choose another loan structure with a shorter term, maybe 3 years. You can also make larger monthly payments. The larger payments will reduce your principal faster- which will also reduce your interest paid on the loan.
Computing Total Interest Using The Simple Interest Formula
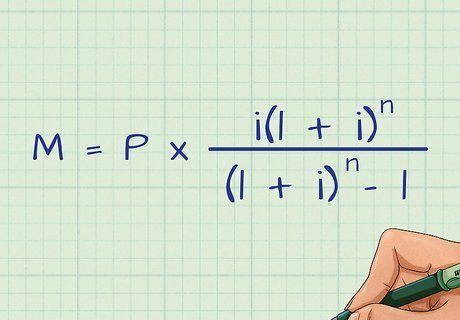
Understand how to calculate total interest. The vast majority of car loans use simple interest. In order to calculate the amount of simple interest you will pay, you’ll first have to calculate your monthly payment using this formula: M = P ∗ i ( 1 + i ) n ( 1 + i ) n − 1 {\displaystyle M=P*{\frac {i(1+i)^{n}}{(1+i)^{n}-1}}} M=P*{\frac {i(1+i)^{n}}{(1+i)^{n}-1}} "M" represents your monthly payment. This is what the formula will be calculating. "P" represents your principal. As previously discussed, this is what you will pay for your car after rebates, trade-ins, and your down payment. "n" represents the total number of monthly payments over the life of the loan. So, if you have a standard, 6-year loan, this would be 6 six years * 12 months per year, or 72. i" represents your monthly interest rate. This is your stated interest rate, usually listed as your APR, divided by 12. So, if your stated interest rate is 6%, your monthly interest rate would be 6%/12, or 0.5%. For the purpose of calculation, this number will have to be represented as a decimal instead of as a percentage. To get this number, simply divide your monthly percent interest by 100. In the example, this would be 0.5%/100, or 0.005.
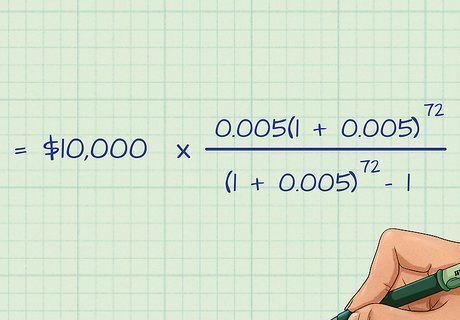
Input your variables into the equation. Even if you don't already have concrete terms for your loan, you can use estimates here and get a good idea of what various different loans would cost you. For example, we can use the terms discussed previously. That is, a loan with $10,000 principal, 6% APR (interest), over 6 years. Our inputs would then be 10,000 for "P," 0.005 (the monthly interest rate, expressed as a decimal) for "i," and 72 (6 years x 12 months per year) for "n." Our example equation would now look as follows: M = 10 , 000 ∗ 0.005 ( 1 + 0.005 ) 72 ( 1 + 0.005 ) 72 − 1 {\displaystyle M=10,000*{\frac {0.005(1+0.005)^{72}}{(1+0.005)^{72}-1}}} M=10,000*{\frac {0.005(1+0.005)^{{72}}}{(1+0.005)^{{72}}-1}}
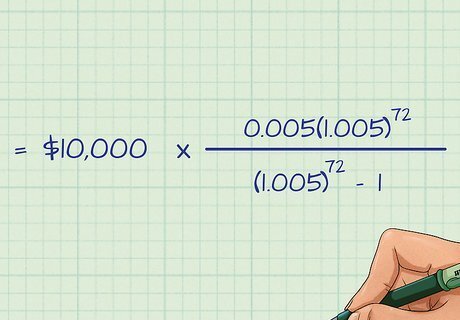
Simplify your equation. From here, you'll simply to have solve your completed equation in the proper order. Start by solving the parts within the parentheses. In this case, this just means adding the 1 to the 0.005 in both places. Your simplified equation should now look like this: M = 10 , 000 ∗ 0.005 ( 1.005 ) 72 ( 1.005 ) 72 − 1 {\displaystyle M=10,000*{\frac {0.005(1.005)^{72}}{(1.005)^{72}-1}}} M=10,000*{\frac {0.005(1.005)^{{72}}}{(1.005)^{{72}}-1}}
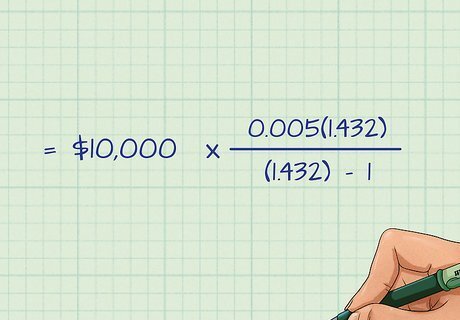
Solve the exponents. Next, you'll have to raise the parts in the parentheses to the power of "n" (72 in this case). This is done on a calculator by typing in the value within parentheses (1.005 in this case) first and then pressing the exponents button, usually denoted as "x^y". You can also type this calculation into Google and it will solve it for you. In our example, we raise 1.005^72 and get 1.432. Our equation now looks as follows: M = 10 , 000 ∗ 0.005 ( 1.432 ) ( 1.432 ) − 1 {\displaystyle M=10,000*{\frac {0.005(1.432)}{(1.432)-1}}} M=10,000*{\frac {0.005(1.432)}{(1.432)-1}}
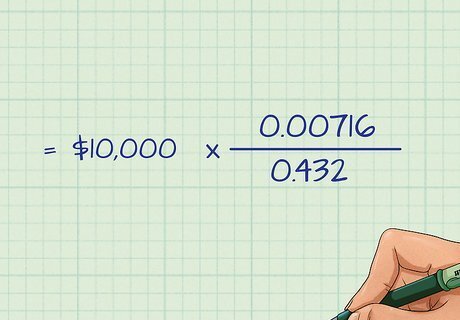
Simplify again. This time, you'll need to simplify the top and bottom parts of the fraction, also called the numerator and denominator, respectively. To simplify, multiply the parts on top and subtract on the bottom. After these calculations, our example equation will look as follows: M = 10 , 000 ∗ 0.00716 ) 0.432 {\displaystyle M=10,000*{\frac {0.00716)}{0.432}}} M=10,000*{\frac {0.00716)}{0.432}}
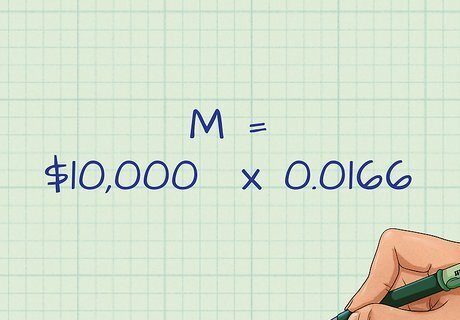
Solve the fraction. Divide the numerator by the denominator. The result is the number that will be multiplied by your principal to determine your monthly payments. After this calculation, our sample equation will simply be M = 10 , 000 ∗ 0.0166 {\displaystyle M=10,000*0.0166} M=10,000*0.0166
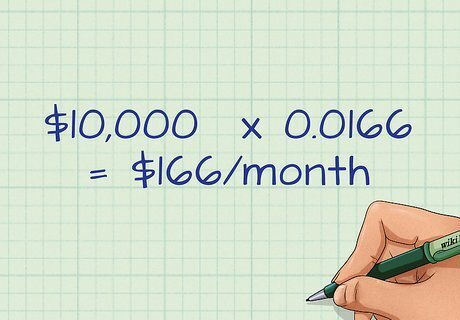
Calculate your monthly payment. Multiply the final two terms in your equation to find your monthly payment. In this case, the monthly payment is $10,000*0.0166, or $166/month. Keep in mind that this number will vary slightly due to rounding during the calculation process.
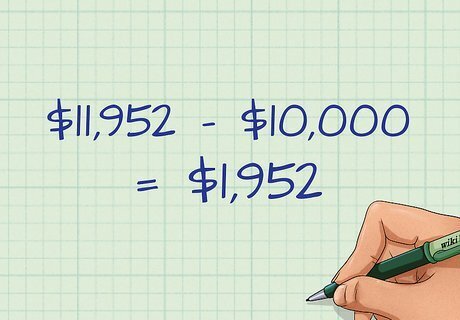
Calculate your total interest paid. This is done by subtracting your principal from the total value of your payments. To get your total value of payments, multiply your number of payments, "n," by the value of your monthly payment, "m." Then, subtract your principal, "P," from this number. The result is your total interest paid on your car loan. In our example, this would be calculated as 72("n") * $166("M")=$11,952 - $10,000 ('P")= $1,952. So, total interest paid on this loan would be $1,952, which accounts for nearly one-fifth of the value of the loan.


















Comments
0 comment