
views
Introducing Basic Division

Present division as a way to share. It’s easier for kids to understand division if they can imagine a set of items being divided equally amongst a group. While 10/5 might seem confusing, giving out 10 cookies to 5 friends makes it seem simple! If you’re teaching your own child, you can introduce division by having them help you divide items into goody bags or separate baked goods into sandwich bags to hand out to friends. In a classroom setting, students can work in groups to divide a number of items, such as candies or plastic bears, evenly among themselves. Most students begin to learn division in the 3rd grade or around the age of 8 or 9.

Explain how you can divide items into smaller, equal groups. Ask your child or your students to divide the same larger number into smaller groups of various sizes. You can use manipulatives, pictures of the items, or a worksheet. This helps them get a better grasp about how basic division works. Manipulatives are any small item that represents the numerical amounts in math problems, such as beans or plastic coins. Your student or child can physically see and touch the items, which helps them better understand the mathematical concepts.

Incorporate the symbols used for division problems. This seems simple, but it’s an easy step to overlook. Remember to talk about both the division sign and the forward slash as a way to signify division. Try writing a division problem down while saying it out loud to reiterate when the symbols should be used. For example, 10 divided by 5 can be written like this: 10/5 or 10÷5. 8 divided by 2 can be written like this: 8/2 or 8÷2.
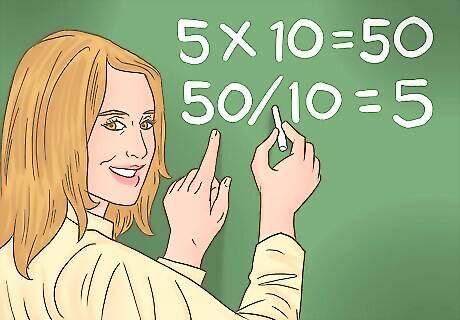
Explain that division is the opposite of multiplication. If your student or your child already knows about multiplication, this is a good scaffolding to build on. Grab a multiplication chart and show them how the times table can be worked backwards using division. For example, go through the 5 times tables, starting at 5 x 10 = 50. Show your student or child that 50/10 = 5. Then go to 5 x 9 = 45, and explain that 45/9 = 5. Continue until you complete the times table. Or, write out the problems on flash cards with the multiplication problem on the front and the division problem on the back. Show your student or child that 2 x 10 = 20 and have them guess the corresponding division problem (20/10 = 2). You can compare the relationship of multiplication and division to addition and subtraction—they're both opposites.

Begin dividing by numbers, starting with 1 and working up to 10. Provide your student or child with a few simple math problems consisting of numbers that divide evenly. Remind them that division effectively creates smaller groups out of a larger sum. You can work backwards from multiplication tables. For example, when dividing by 3, the math problems would include 3/3, 6/3, 9/3, 12/3, 15/3, etc. At this point, make sure the numbers divide evenly.

Solidify the concepts with some worksheets. You can download free worksheets to use for practice by searching online for "division worksheets," or you can create your own. For beginners, focus on numerical problems. However, they may benefit from illustrations or context. If you’re making your own worksheets, you might make a worksheet about dividing pizza for a party. The context is that the student must divide certain numbers of pizza slices per varying numbers of guests, but the math problems will contain just numbers, such as 12/3, 12/4, 24/8, etc. EXPERT TIP Joseph Meyer Joseph Meyer Math Teacher Joseph Meyer is a High School Math Teacher based in Pittsburgh, Pennsylvania. He is an educator at City Charter High School, where he has been teaching for over 7 years. Joseph is also the founder of Sandbox Math, an online learning community dedicated to helping students succeed in Algebra. His site is set apart by its focus on fostering genuine comprehension through step-by-step understanding (instead of just getting the correct final answer), enabling learners to identify and overcome misunderstandings and confidently take on any test they face. He received his MA in Physics from Case Western Reserve University and his BA in Physics from Baldwin Wallace University. Joseph Meyer Joseph Meyer Math Teacher Combine traditional methods with online tools to teach math. Traditional methods like manipulatives provide a strong foundation for younger students. As they progress, well-designed online tools can offer engaging visualizations and promote problem-solving skills, complementing, not replacing, traditional methods.
Adding Remainders

Explain that remainders occur when you can’t divide evenly. Once your student or child has a firm grasp on the basics of division, they’re ready to work with remainders. After you explain the concept, you can help your student understand it by working with manipulatives. For example, you might say that your student or child has 10 cookies to share with 3 friends. This would allow them to give 3 cookies to each friend, leaving 1 extra cookie. This cookie is the remainder.
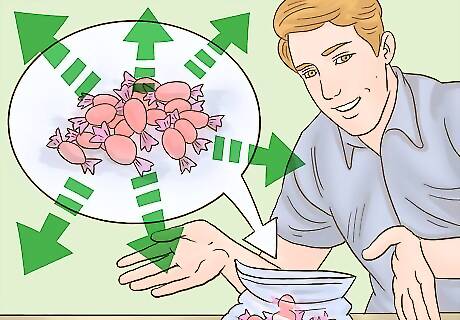
Work through a few basic problems using manipulatives. Count out a certain number of a manipulative, such as candies, plastic coins, blocks, beans, or poker chips. Then, ask your student or child to divide the items into various sizes of groups. If the items can’t be divided evenly, have them create a “remainder” group. For example, you could ask them to divide 25 candies into various groups. While 5 groups would divide evenly, 4 groups wouldn’t. This would leave 1 extra candy, since 4 doesn’t go into 25 evenly.

Ask your student or child to describe why they have a remainder. Explaining the remainder to you will help solidify the concept. If necessary, you can help them walk through the reasoning. Then, ask them to divide another set of items and explain the remainder without your help. Ask, “Why do you have 1 candy left?” Help them arrive at the answer, which is that 4 doesn’t go into 25 evenly. You could say, "How many cookies would 4 each friends get if the package had 25?" or "Would 4 people be able to split 25 cookies evenly?" Finally, explain that 1 is the remainder. If they still cannot explain it without help, switch to a new problem and continue to work through the exercise until they are able to explain remainders without your help.

Print out a few practice worksheets. You can find free practice worksheets online, or you can make them yourself. This will help them learn to work though the concepts they’ve learned on paper. If you make your own worksheets, focus primarily on numerical problems. However, you can also include a few word problems at the bottom. You might start by providing them with the same problems they’ve already worked through with their manipulatives. This allows them to see how their real world experience with the items relates to written math problems.
Teaching Long Division
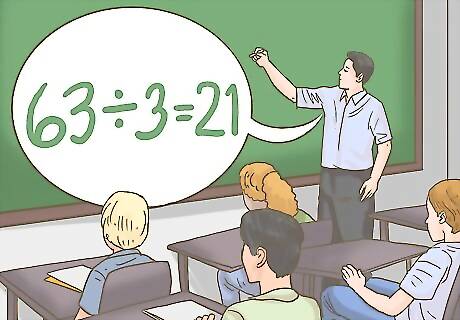
Start with numbers that divide evenly. Long division is easier to understand if you start with a large number that can be divided without any remainders. This will explain the process for working though the problem without any complicating factors. For example, 63/3=21. The 3 will go into the 6 evenly, then the 3 will go into the 3 evenly. There are no remainders on either step. Most kids will begin learning long division in 3rd grade, or around the age of 8 or 9.
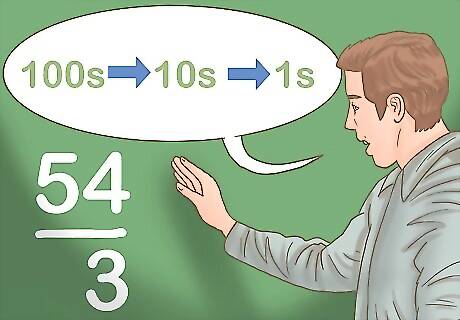
Explain how to divide the divisor into the first number of the dividend. The divisor is the number that you are dividing by, while the dividend is the number you’re dividing into. Tell your student or child that they will need to divide each unit in the dividend by the divisor, starting with the largest unit. For example, you’d divide the 100s unit, then the 10s unit, and finally the 1s unit. Let’s say your problem is 54/3. Your divisor is 3, which goes into 5 just 1 time. However, you are left with a remainder of 2, which you will need to save for the next step. Similarly, let’s say your problem is 155/4. You can’t divide 4 into 1, so you’d divide it into 15. This would give you 3, with a remainder of 3.
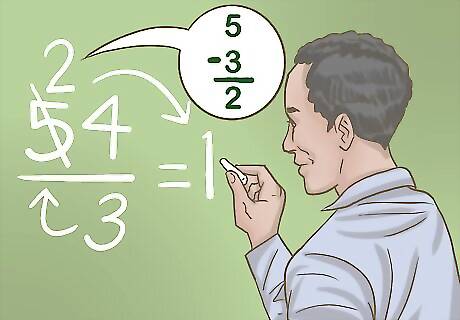
Show your student or child how to find the remainder to carry over. Explain that they will need to multiply the number of times that the divisor goes into the first number by the divisor. They will subtract this product from the units in the dividend to find the remainder, which they’ll carry over to the next unit. As you work though 54/3, you know that 3 goes into 5 just 1 time with a remainder of 2. You’d multiply 3 x 1 = 3. Subtract 3 from 5 to get 2. Leave the 2 in the 10s spot. Similarly, for 155/4, you know that 4 goes into 15 just 3 times. You’d multiply 4 x 3 = 12. Subtract 15-12= 3. Carry the 3 down in the 10s spot.
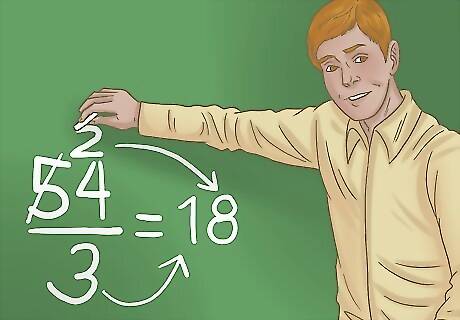
Divide the divisor into the next number, including any remainder. Carry the next unit down, adding it to the remainder. Then, divide the divisor into this number. Write the result into your answer, and then subtract to find your remainder, if you have one. Working through 54/3, you will carry the 4 down, writing it next to the 2, which gives you 24. You’ll next divide 3 into 24. This gives you 8. Putting it all together, your answer is 54/3=18. Similarly, as you work through 155/4, you’d now have a 3 left in your 10s spot. Carry down the 5, to give you 35. Divide the 4 into 35, which will give you a result of 8, with 3 remaining.

Continue working the problem until you arrive at your answer. Explain that the number of steps you’ll take depends on how many numbers are in the dividend. For example, 155/3 will have fewer steps than 1555/3. However, the process for each unit remains the same.
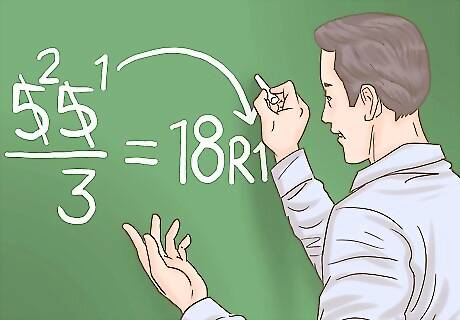
Demonstrate how to find the remainder. Once your student or child has divided the divisor into the 1s place, they’ve reached the end of the problem. If the divisor does not go in evenly, there will be a remainder. They’ll need to include this remainder in their answer. Since 3 goes into 54 evenly, you don’t have a remainder. However, 55/3 would give you a remainder of 1. You would find this remainder like this: If you divide 3 into 5, you get 1, with 2 remaining. You’d then divide 3 into 25, which would give you 8, with 1 remaining. This is your remainder.

Show them how to write a remainder, if there is one. Your remainder should be written as part of your answer. You can indicate that it’s a remainder by writing “R” in front of it. Alternatively, you may write out the word “Remainder" followed by the number. For example, you’d write 55/3=18 R 1 or 55/3=18 Remainder 1.
Provide practice problems to help them work through the steps. Lots of practice is essential for mastering math concepts. You can create your own worksheets or download them for free online. You could provide your student or child with real world scenarios to help them practice long division. For example, they could practice dividing large quantities of food among party guests. Similarly, you could have them divide their birthday money into 3 categories: spend now, save for later, save for college.
Playing Math Games

Read books about division with young children. Stories are a great way for kids to learn about a new concept, and a picture book will keep young children engaged. Ask them to pick out the story they’d most like to read. Here are some great options: Count on Pablo by Barbara deRubertis The Great Divide by Dayle Ann Dodds Divide and Ride by Stuart J. Murphy 2 X 2 = Boo: A Set of Spooky Multiplication Stories by Loreen Leedy Arctic Fives Arrive by Elinor J. Pinczes Bean Thirteen by Matthew McElligott

Work on dividing food for basic division practice. You can use pretend food or real food to help young learners understand how to do basic division. Here are some ways they can divide the food: Ask them to divide the food equally. Have them divide the food for various groups, such as 2, 4, 5, or 10 friends. Make a recipe with the student but ask them to do the math to reduce the number of servings. Remember—students learn in lots of different ways! Some kids might find a hands-on approach helpful.

Divide a set of toys to understand remainders. They could divide stuffed animals, Legos, dolls, army men, or even blocks. Ask them to create subsets among their toys, or have them divide the toys into groups. For example, ask them to divide all stuffed bears into groups of 3, with remainders set aside. Similarly, all red Legos can be divided into groups of 5, with remainders set aside.


















Comments
0 comment