How to Find the Perimeter of a Polygon

Finding the Perimeter of a Regular Polygon

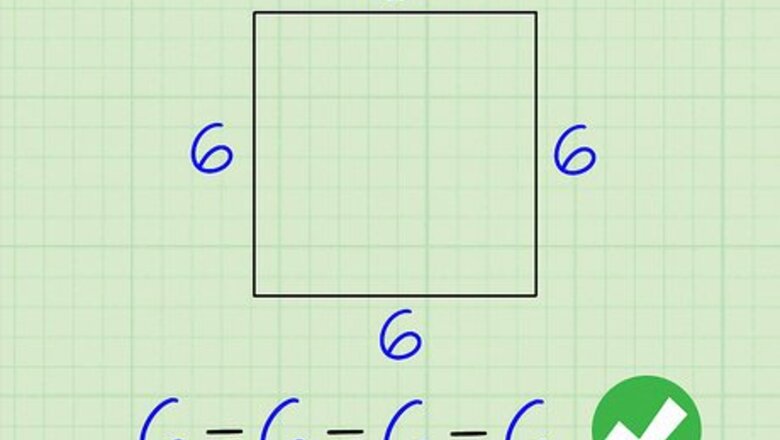
Check that the sides of the polygon are all the same length. Regular polygons are polygons that have equal sides. If the sides of the polygon you’re looking at aren’t all the same length, you’ll need to find the perimeter using the method for irregular polygons instead. If the side lengths are equal, you’re working with a regular polygon.Tip: If some of the sides aren't labeled, try looking at the rest of the polygon to determine what the lengths are. For example, if you have a square with only 1 labeled side, you know the other sides are the same length since squares have equal sides.

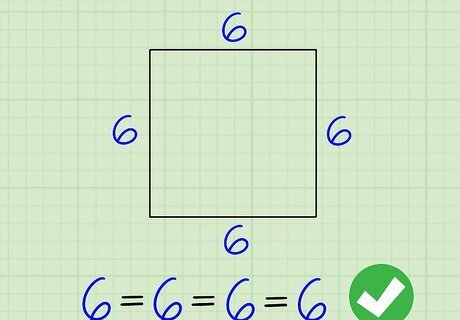
Write down the length of 1 side of the polygon. It doesn’t matter which side you choose since all of the side lengths are equal. Just make sure you’re only writing down the length of 1 side. For example, if you're working with a square that has a side length of 6, you would write down “6.”

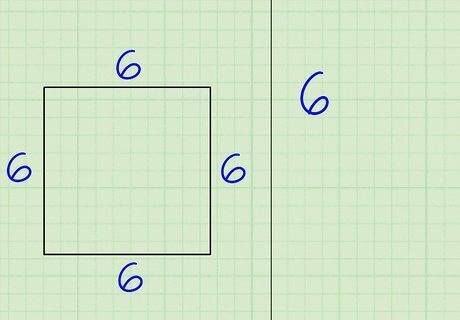
Write down the total number of sides that the polygon has. Don’t worry about the side lengths at this point. Just count how many sides the polygon has and write it down. For a square, you’d write down “4” since a square has 4 sides.

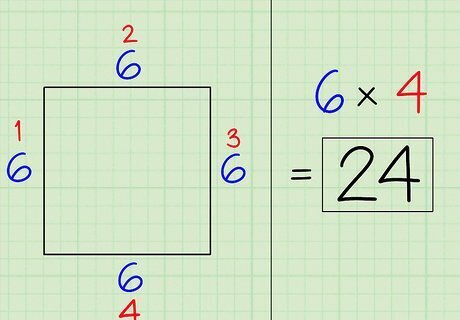
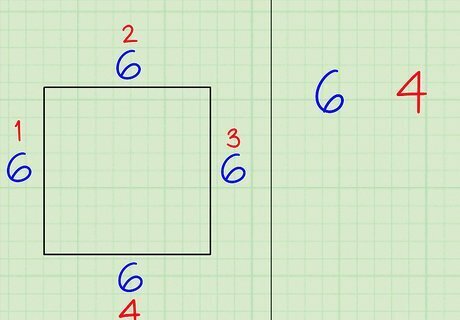
Multiply the side length by the number of sides to get the perimeter. The formula for finding the perimeter of a regular polygon is just the number of sides x the length of any side. Once you’ve multiplied those 2 numbers together, you’ve found the perimeter of the polygon! In the square example, you know that the square has a side length of 6 and a total of 4 sides. Therefore, you'd just multiply 6 by 4 to get 24, which would be the perimeter of the square. Or, say you were working with a triangle that has a side length of 3. Since a triangle has 3 sides, you would multiply 3 (the number of sides) by 3 (the side length) to get 9. Therefore, the perimeter of the triangle would be 9.

Calculating the Perimeter of an Irregular Polygon

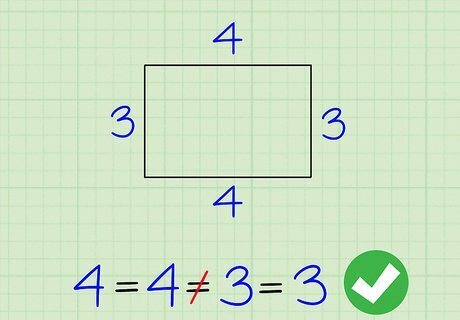
Look at the length of the polygon’s sides to determine if it’s irregular. An irregular polygon is a polygon that doesn’t have equal sides. If the sides of the polygon are all the same length, that means the polygon is regular, not irregular.Did you know? You can use the same method for finding the perimeter of an irregular polygon to find the perimeter of a regular polygon, but not the other way around.

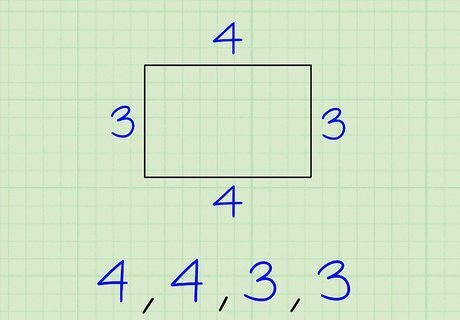
Write down the length of each side of the polygon. Since not all sides of an irregular polygon are equal, you’ll need to write out each individual side length. Even if some of the sides are equal, you should still write each length out individually. For example, if you’re working with a rectangle that has 2 sides that are 4 units long and 2 sides that are 3 units long, you would write “4, 4, 3, 3.” If you’re working with an irregular polygon that has 1 side that’s 2 units, 1 side that’s 3 units, and 1 side that’s 4 units, you would write “2, 3, 4.”

Add up all of the lengths to find the perimeter. To find the perimeter of an irregular polygon, all you need to do is find the total of all of its side lengths. Simply add up each side length that you wrote down to find the perimeter of the polygon! For example, if the side lengths for the polygon were 4, 4, 3, and 3, they would add up to 14. Therefore, 14 would be the perimeter of the polygon.

Determining Perimeter Using Given Coordinates

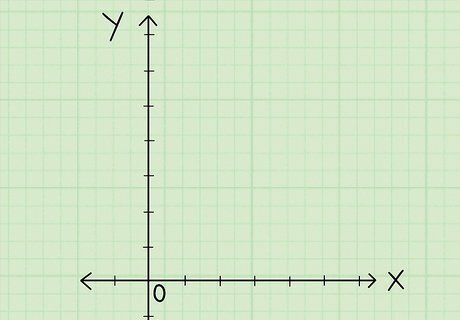
Draw a coordinate grid with an x- and y-axis. A coordinate grid is a graph with an x- and y-axis that you can plot coordinates on. To draw a coordinate grid, get a piece of graph paper or draw your own grid lines on a blank piece of paper using a ruler. Then, draw a horizontal line through the middle for the x-axis and a vertical line down the center for the y-axis. Finally, number the points on each axis, starting with “0” where the x- and y-axis intersect. When you number your grid, the numbers above and to the right of the 0 will be positive, while the numbers below and to the left of the 0 will be negative.

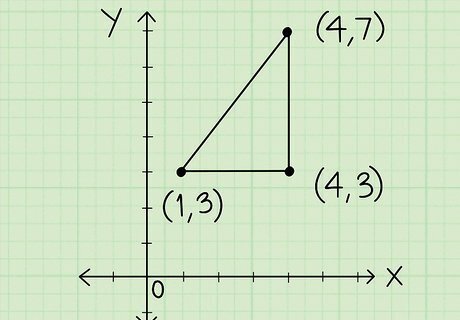
Plot the given coordinates on the graph. You should have been given coordinates for each vertex, or angular point, of the polygon you’re trying to find the perimeter of. Each coordinate should look something like “(1,2)." Use the numbers you marked on the coordinate grid to plot each of the coordinates. When you’re finished, connect the points with straight lines to see the shape of the polygon you’re working with.Tip: When plotting coordinates, remember that the first number represents the x-axis and the second number represents the y-axis. For example, if you were plotting (2,4), you would count 2 over on the x-axis and 4 up on the y-axis and then mark where those 2 points meet on the grid.

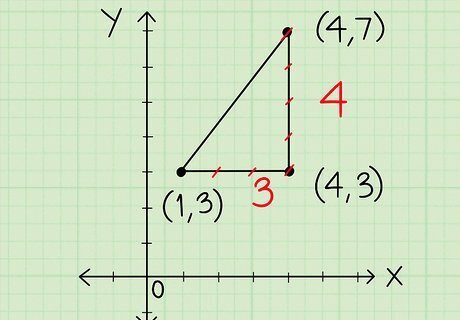
Find vertical and horizontal side lengths by counting the units. You’ll need to know the length of each side of the polygon to determine its perimeter. For vertical or horizontal sides, simply count how many units there are between the points on each end. Then, write down the number next to that side so you can refer to it later. For example, if you’re trying to find the length of a horizontal side, start at one end and count the number of boxes between that point and the other end. If you counted 6, that would mean the length of that side is 6 units.

Use the distance formula to find the length of diagonal sides. Unfortunately, you can’t count the units on a grid to find the length of diagonal sides like you can with vertical or horizontal sides. Instead, you’ll need to use the distance formula, which is d = ( x 2 − x 1 ) 2 + ( y 2 − y 1 ) 2 {\displaystyle d={\sqrt {(x_{2}-x_{1})^{2}+(y_{2}-y_{1})^{2}}}} d={\sqrt {(x_{{2}}-x_{{1}})^{{2}}+(y_{{2}}-y_{{1}})^{{2}}}}. Just plug in the values of the x and y coordinates for the 2 points at the ends of the side you’re trying to find the distance of and solve to find the length. For example, if you’re trying to find the distance (length) between 2 points with the coordinates (4,7) and (1,3), you would plug those coordinates into the formula and get d = ( 4 2 − 1 1 ) 2 + ( 7 2 − 3 1 ) 2 {\displaystyle d={\sqrt {(4_{2}-1_{1})^{2}+(7_{2}-3_{1})^{2}}}} d={\sqrt {(4_{{2}}-1_{{1}})^{{2}}+(7_{{2}}-3_{{1}})^{{2}}}} Then, you would simplify the equation to get d = 25 {\displaystyle d={\sqrt {25}}} d={\sqrt {25}}. Finally, you would solve d = 25 {\displaystyle d={\sqrt {25}}} d={\sqrt {25}} and get 5. Therefore, the length of the side would be 5.

Add the length of each side together to find the polygon’s perimeter. The perimeter of a polygon is equal to the sum of all of its side lengths. Once you’ve determined all of these lengths using the coordinates you were given, all you need to do is add them together and then you’re done! For example, if you plotted the coordinates of a triangle and found that the side lengths are 3, 2, and 5, you would add these numbers together to get 10. Therefore, the perimeter of the triangle is 10.