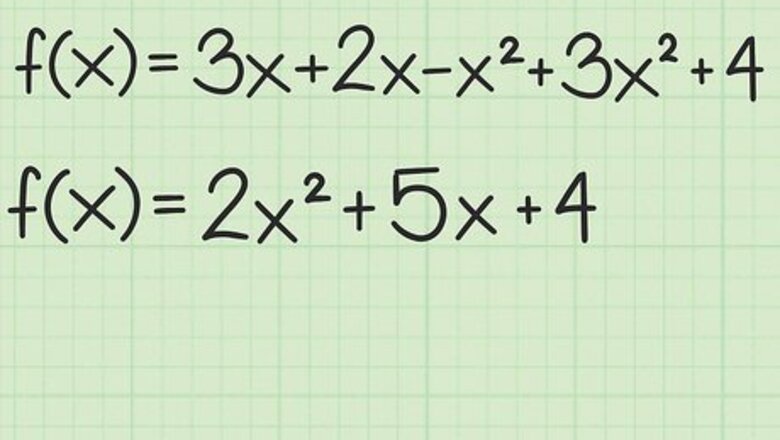
views
f
(
x
)
=
a
x
2
+
b
x
+
c
{\displaystyle f(x)=ax^{2}+bx+c}
, or in standard form,
f
(
x
)
=
a
(
x
−
h
)
2
+
k
{\displaystyle f(x)=a(x-h)^{2}+k}
. Finally, you may also wish to use some basic calculus to define the maximum or minimum of any quadratic function.
Beginning with the General Form of the Function
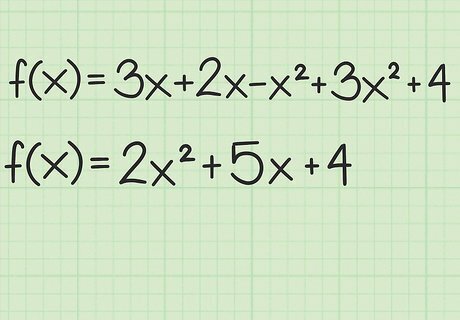
Set up the function in general form. A quadratic function is one that has an x 2 {\displaystyle x^{2}} x^{2} term. It may or may not contain an x {\displaystyle x} x term without an exponent. There will be no exponents larger than 2. The general form is f ( x ) = a x 2 + b x + c {\displaystyle f(x)=ax^{2}+bx+c} f(x)=ax^{2}+bx+c. If necessary, combine similar terms and rearrange to set the function in this general form. For example, suppose you start with f ( x ) = 3 x + 2 x − x 2 + 3 x 2 + 4 {\displaystyle f(x)=3x+2x-x^{2}+3x^{2}+4} f(x)=3x+2x-x^{2}+3x^{2}+4. Combine the x 2 {\displaystyle x^{2}} x^{2} terms and the x {\displaystyle x} x terms to get the following in general form: f ( x ) = 2 x 2 + 5 x + 4 {\displaystyle f(x)=2x^{2}+5x+4} f(x)=2x^{2}+5x+4
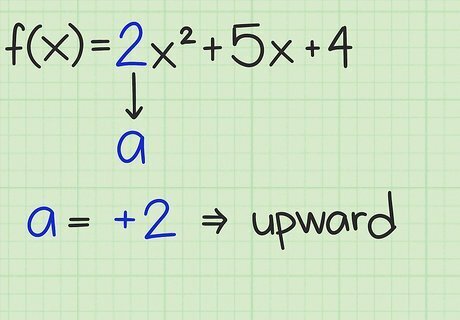
Determine the direction of the graph. A quadratic function results in the graph of a parabola. The parabola either opens upward or downward. If a {\displaystyle a} a, the coefficient of the x 2 {\displaystyle x^{2}} x^{2} term, is positive, then the parabola opens upward. If a {\displaystyle a} a is negative, then the parabola opens downward. Look at the following examples: For f ( x ) = 2 x 2 + 4 x − 6 {\displaystyle f(x)=2x^{2}+4x-6} f(x)=2x^{2}+4x-6, a = 2 {\displaystyle a=2} a=2 so the parabola opens upward. For f ( x ) = − 3 x 2 + 2 x + 8 {\displaystyle f(x)=-3x^{2}+2x+8} f(x)=-3x^{2}+2x+8, a = − 3 {\displaystyle a=-3} a=-3 so the parabola opens downward. For f ( x ) = x 2 + 6 {\displaystyle f(x)=x^{2}+6} f(x)=x^{2}+6, a = 1 {\displaystyle a=1} a=1 so the parabola opens upward. If the parabola opens upward, you will be finding its minimum value. If the parabola opens downward, you will find its maximum value.
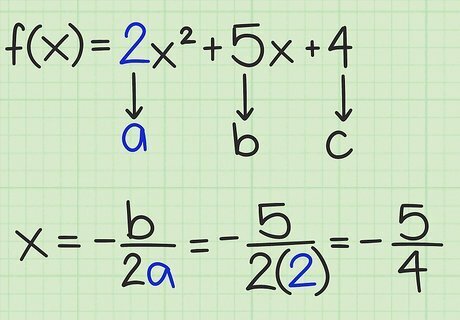
Calculate -b/2a. The value of − b 2 a {\displaystyle -{\frac {b}{2a}}} -{\frac {b}{2a}} tells you the x {\displaystyle x} x value of the vertex of the parabola. When the quadratic function is written in its general form of a x 2 + b x + c {\displaystyle ax^{2}+bx+c} ax^{2}+bx+c, use the coefficients of the x {\displaystyle x} x and x 2 {\displaystyle x^{2}} x^{2} terms as follows: For a function f ( x ) = x 2 + 10 x − 1 {\displaystyle f(x)=x^{2}+10x-1} f(x)=x^{2}+10x-1, a = 1 {\displaystyle a=1} a=1 and b = 10 {\displaystyle b=10} b=10. Therefore, find the x-value of the vertex as: x = − b 2 a {\displaystyle x=-{\frac {b}{2a}}} x=-{\frac {b}{2a}} x = − 10 ( 2 ) ( 1 ) {\displaystyle x=-{\frac {10}{(2)(1)}}} x=-{\frac {10}{(2)(1)}} x = − 10 2 {\displaystyle x=-{\frac {10}{2}}} x=-{\frac {10}{2}} x = − 5 {\displaystyle x=-5} x=-5 As a second example, consider the function f ( x ) = − 3 x 2 + 6 x − 4 {\displaystyle f(x)=-3x^{2}+6x-4} f(x)=-3x^{2}+6x-4. In this example, a = − 3 {\displaystyle a=-3} a=-3 and b = 6 {\displaystyle b=6} b=6. Therefore, find the x-value of the vertex as: x = − b 2 a {\displaystyle x=-{\frac {b}{2a}}} x=-{\frac {b}{2a}} x = − 6 ( 2 ) ( − 3 ) {\displaystyle x=-{\frac {6}{(2)(-3)}}} x=-{\frac {6}{(2)(-3)}} x = − 6 − 6 {\displaystyle x=-{\frac {6}{-6}}} x=-{\frac {6}{-6}} x = − ( − 1 ) {\displaystyle x=-(-1)} x=-(-1) x = 1 {\displaystyle x=1} x=1
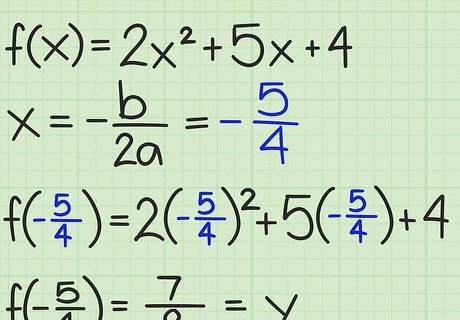
Find the corresponding f(x) value. Insert the value of x that you just calculated into the function to find the corresponding value of f(x). This will be the minimum or maximum of the function. For the first example above, f ( x ) = x 2 + 10 x − 1 {\displaystyle f(x)=x^{2}+10x-1} f(x)=x^{2}+10x-1, you calculated the x-value for the vertex to be x = − 5 {\displaystyle x=-5} x=-5. Enter − 5 {\displaystyle -5} -5 in place of x {\displaystyle x} x in the function to find the maximum value: f ( x ) = x 2 + 10 x − 1 {\displaystyle f(x)=x^{2}+10x-1} f(x)=x^{2}+10x-1 f ( − 5 ) = ( − 5 ) 2 + 10 ( − 5 ) − 1 {\displaystyle f(-5)=(-5)^{2}+10(-5)-1} {\displaystyle f(-5)=(-5)^{2}+10(-5)-1} f ( − 5 ) = 25 − 50 − 1 {\displaystyle f(-5)=25-50-1} {\displaystyle f(-5)=25-50-1} f ( − 5 ) = − 26 {\displaystyle f(-5)=-26} {\displaystyle f(-5)=-26} For the second example above, f ( x ) = − 3 x 2 + 6 x − 4 {\displaystyle f(x)=-3x^{2}+6x-4} f(x)=-3x^{2}+6x-4, you found the vertex to be at x = 1 {\displaystyle x=1} x=1. Insert 1 {\displaystyle 1} 1 in place of x {\displaystyle x} x in the function to find the maximum value: f ( x ) = − 3 x 2 + 6 x − 4 {\displaystyle f(x)=-3x^{2}+6x-4} f(x)=-3x^{2}+6x-4 f ( 1 ) = − 3 ( 1 ) 2 + 6 ( 1 ) − 4 {\displaystyle f(1)=-3(1)^{2}+6(1)-4} {\displaystyle f(1)=-3(1)^{2}+6(1)-4} f ( 1 ) = − 3 + 6 − 4 {\displaystyle f(1)=-3+6-4} {\displaystyle f(1)=-3+6-4} f ( 1 ) = − 1 {\displaystyle f(1)=-1} f(1)=-1
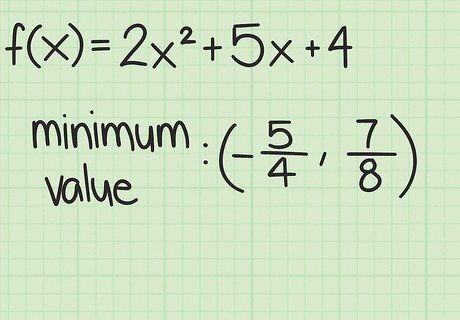
Report your results. Review the question you have been asked. If you are asked for the coordinates of the vertex, you need to report both the x {\displaystyle x} x and y {\displaystyle y} y (or f ( x ) {\displaystyle f(x)} f(x)) values. If you are only asked for the maximum or minimum, you only need to report the y {\displaystyle y} y (or f ( x ) {\displaystyle f(x)} f(x)) value. Refer back to the value of the a {\displaystyle a} a coefficient to be sure if you have a maximum or a minimum. For the first example, f ( x ) = x 2 + 10 x − 1 {\displaystyle f(x)=x^{2}+10x-1} f(x)=x^{2}+10x-1, the value of a {\displaystyle a} a is positive, so you will be reporting the minimum value. The vertex is at ( − 5 , − 26 ) {\displaystyle (-5,-26)} (-5,-26), and the minimum value is − 26 {\displaystyle -26} -26. For the second example, f ( x ) = − 3 x 2 + 6 x − 4 {\displaystyle f(x)=-3x^{2}+6x-4} f(x)=-3x^{2}+6x-4, the value of a {\displaystyle a} a is negative, so you will be reporting the maximum value. The vertex is at ( 1 , − 1 ) {\displaystyle (1,-1)} (1,-1), and the maximum value is − 1 {\displaystyle -1} -1.
Using the Standard or Vertex Form
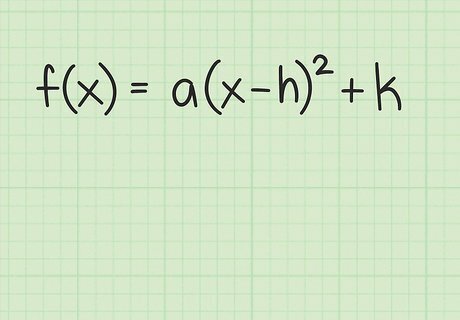
Write your quadratic function in standard or vertex form. The standard form of a general quadratic function, which can also be called the vertex form, looks like this: f ( x ) = a ( x − h ) 2 + k {\displaystyle f(x)=a(x-h)^{2}+k} f(x)=a(x-h)^{2}+k If your function is already given to you in this form, you just need to recognize the variables a {\displaystyle a} a, h {\displaystyle h} h and k {\displaystyle k} k. If your function begins in the general form f ( x ) = a x 2 + b x + c {\displaystyle f(x)=ax^{2}+bx+c} f(x)=ax^{2}+bx+c, you will need to complete the square to rewrite it in vertex form. To review how to complete the square, see Complete the Square.
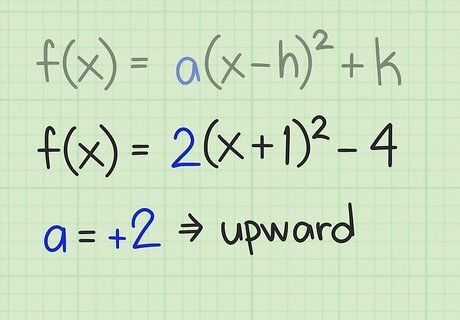
Determine the direction of the graph. Just as with a quadratic function written in its general form, you can tell the direction of the parabola by looking at the coefficient a {\displaystyle a} a. If a {\displaystyle a} a in this standard form is positive, then the parabola opens upward. If a {\displaystyle a} a is negative, then the parabola opens downward. Look at the following examples: For f ( x ) = 2 ( x + 1 ) 2 − 4 {\displaystyle f(x)=2(x+1)^{2}-4} f(x)=2(x+1)^{2}-4, a = 2 {\displaystyle a=2} a=2, which is positive, so the parabola opens upward. For f ( x ) = − 3 ( x − 2 ) 2 + 2 {\displaystyle f(x)=-3(x-2)^{2}+2} f(x)=-3(x-2)^{2}+2, a = − 3 {\displaystyle a=-3} a=-3, which is negative, so the parabola opens downward. If the parabola opens upward, you will be finding its minimum value. If the parabola opens downward, you will find its maximum value.
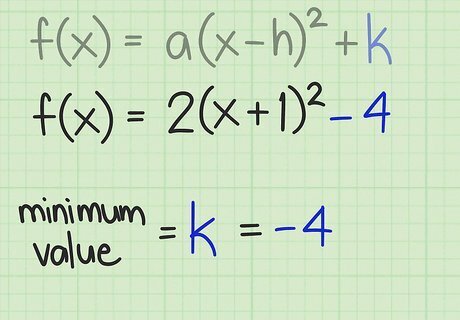
Identify the minimum or maximum value. When the function is written in standard form, finding the minimum or maximum value is as simple as stating the value of the variable k {\displaystyle k} k. For the two example functions given above, these values are: For f ( x ) = 2 ( x + 1 ) 2 − 4 {\displaystyle f(x)=2(x+1)^{2}-4} f(x)=2(x+1)^{2}-4, k = − 4 {\displaystyle k=-4} k=-4. This is the minimum value of the function because this parabola opens upward. For f ( x ) = − 3 ( x − 2 ) 2 + 2 {\displaystyle f(x)=-3(x-2)^{2}+2} f(x)=-3(x-2)^{2}+2, k = 2 {\displaystyle k=2} k=2. This is the maximum value of the function, because this parabola opens downward.
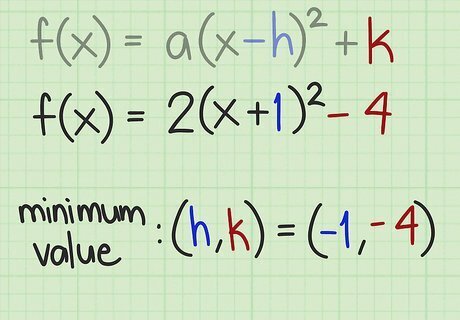
Find the vertex. If you are asked for the coordinates of the minimum or maximum value, the point will be ( h , k ) {\displaystyle (h,k)} (h,k). Note, however, that in the standard form of the equation, the term inside the parentheses is ( x − h ) {\displaystyle (x-h)} (x-h), so you need the opposite sign of the number that follows the x {\displaystyle x} x. For f ( x ) = 2 ( x + 1 ) 2 − 4 {\displaystyle f(x)=2(x+1)^{2}-4} f(x)=2(x+1)^{2}-4, the term inside the parentheses is (x+1), which can be rewritten as (x-(-1)). Thus, h = − 1 {\displaystyle h=-1} h=-1. Therefore, the coordinates of the vertex for this function are ( − 1 , − 4 ) {\displaystyle (-1,-4)} (-1,-4). For f ( x ) = − 3 ( x − 2 ) 2 + 2 {\displaystyle f(x)=-3(x-2)^{2}+2} f(x)=-3(x-2)^{2}+2, the term inside the parentheses is (x-2). Therefore, h = 2 {\displaystyle h=2} h=2. The coordinates of the vertex are (2, 2).
Using Calculus to Derive the Minimum or Maximum
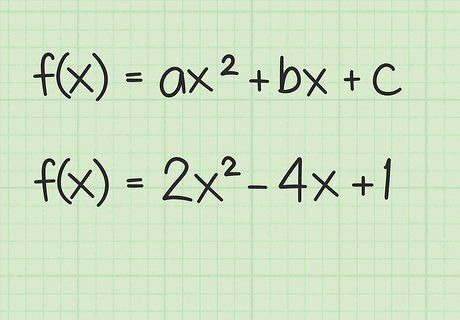
Start with the general form. Write your quadratic function in general form, f ( x ) = a x 2 + b x + c {\displaystyle f(x)=ax^{2}+bx+c} f(x)=ax^{2}+bx+c. If necessary, you may need to combine like terms and rearrange to get the proper form. Begin with the sample function f ( x ) = 2 x 2 − 4 x + 1 {\displaystyle f(x)=2x^{2}-4x+1} f(x)=2x^{2}-4x+1.
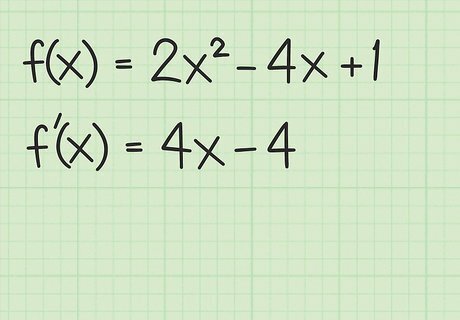
Use the power rule to find the first derivative. Using basic first-year calculus, you can find the first derivative of the general quadratic function to be f ′ ( x ) = 2 a x + b {\displaystyle f^{\prime }(x)=2ax+b} f^{{\prime }}(x)=2ax+b. For the sample function f ( x ) = 2 x 2 − 4 x + 1 {\displaystyle f(x)=2x^{2}-4x+1} f(x)=2x^{2}-4x+1, find the derivative as: f ′ ( x ) = 4 x − 4 {\displaystyle f^{\prime }(x)=4x-4} f^{{\prime }}(x)=4x-4
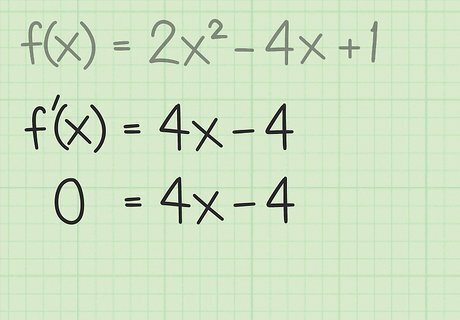
Set the derivative equal to zero. Recall that derivative of a function tells you the slope of the function at that selected point. The minimum or maximum of a function occurs when the slope is zero. Therefore, to find where the minimum or maximum occurs, set the derivative equal to zero. Continue with the sample problem from above: f ′ ( x ) = 4 x − 4 {\displaystyle f^{\prime }(x)=4x-4} f^{{\prime }}(x)=4x-4 0 = 4 x − 4 {\displaystyle 0=4x-4} 0=4x-4
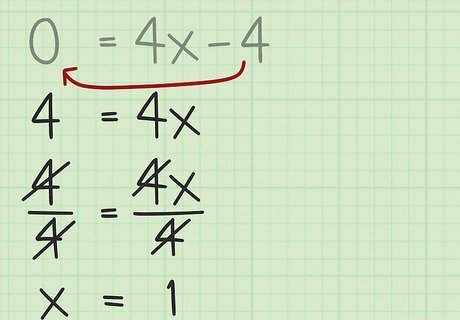
Solve for x. Use basic rules of algebra to rearrange the function and solve the value for x, when the derivative equals zero. This solution will tell you the x-coordinate of the vertex of the function, which is where the maximum or minimum will occur. 0 = 4 x − 4 {\displaystyle 0=4x-4} 0=4x-4 4 = 4 x {\displaystyle 4=4x} 4=4x 1 = x {\displaystyle 1=x} 1=x
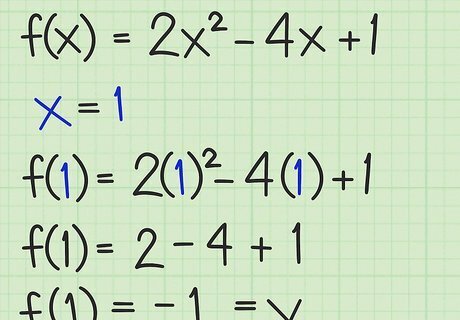
Insert the solved value of x into the original function. The minimum or maximum value of the function will be the value for f ( x ) {\displaystyle f(x)} f(x) at the selected x {\displaystyle x} x position. Insert your value of x {\displaystyle x} x into the original function and solve to find the minimum or maximum. For the function f ( x ) = 2 x 2 − 4 x + 1 {\displaystyle f(x)=2x^{2}-4x+1} f(x)=2x^{2}-4x+1 at x = 1 {\displaystyle x=1} x=1, f ( 1 ) = 2 ( 1 ) 2 − 4 ( 1 ) + 1 {\displaystyle f(1)=2(1)^{2}-4(1)+1} f(1)=2(1)^{2}-4(1)+1 f ( 1 ) = 2 − 4 + 1 {\displaystyle f(1)=2-4+1} f(1)=2-4+1 f ( 1 ) = − 1 {\displaystyle f(1)=-1} f(1)=-1

Report your solution. The solution gives you the vertex of the maximum or minimum point. For this sample function, f ( x ) = 2 x 2 − 4 x + 1 {\displaystyle f(x)=2x^{2}-4x+1} f(x)=2x^{2}-4x+1, the vertex occurs at ( 1 , − 1 ) {\displaystyle (1,-1)} (1,-1). The coefficient a {\displaystyle a} a is positive, so the function opens upward. Therefore, the minimum value of the function is the y-coordinate of the vertex, which is − 1 {\displaystyle -1} -1.

















Comments
0 comment