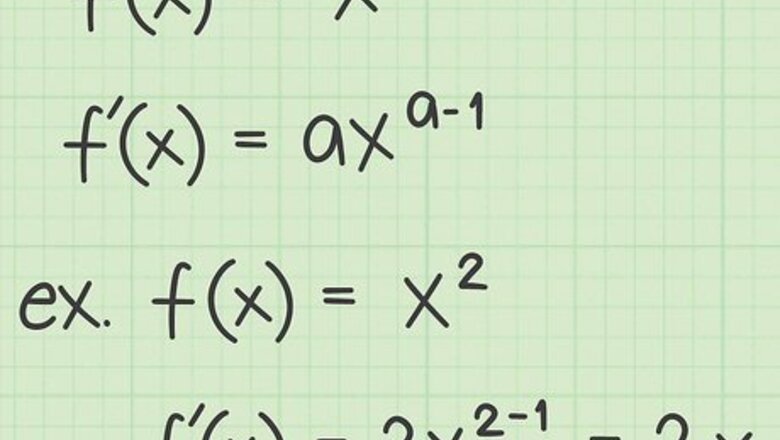
views
x
{\displaystyle {\sqrt {x}}}
, the power rule seems difficult to apply. Using a simple exponent substitution, differentiating this function becomes very straightforward. You can then apply the same substitution and use the chain rule of calculus to differentiate many other functions that include radicals.
Using the Power Rule
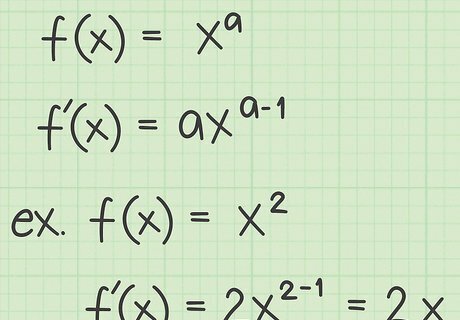
Review the power rule for derivatives. The first rule you probably learned for finding derivatives is the power rule. This rule says that for a variable x {\displaystyle x} x raised to any exponent a {\displaystyle a} a, the derivative is as follows: f ( x ) = x a {\displaystyle f(x)=x^{a}} f(x)=x^{{a}} f ′ ( x ) = a x a − 1 {\displaystyle f^{\prime }(x)=ax^{a-1}} f^{{\prime }}(x)=ax^{{a-1}} For example, review the following functions and their derivatives: If f ( x ) = x 2 {\displaystyle f(x)=x^{2}} f(x)=x^{2}, then f ′ ( x ) = 2 x {\displaystyle f^{\prime }(x)=2x} f^{{\prime }}(x)=2x If f ( x ) = 3 x 2 {\displaystyle f(x)=3x^{2}} f(x)=3x^{2}, then f ′ ( x ) = 2 ∗ 3 x = 6 x {\displaystyle f^{\prime }(x)=2*3x=6x} f^{{\prime }}(x)=2*3x=6x If f ( x ) = x 3 {\displaystyle f(x)=x^{3}} f(x)=x^{3}, then f ′ ( x ) = 3 x 2 {\displaystyle f^{\prime }(x)=3x^{2}} f^{{\prime }}(x)=3x^{2} If f ( x ) = 1 2 x 4 {\displaystyle f(x)={\frac {1}{2}}x^{4}} f(x)={\frac {1}{2}}x^{4}, then f ′ ( x ) = 4 ∗ 1 2 x 3 = 2 x 3 {\displaystyle f^{\prime }(x)=4*{\frac {1}{2}}x^{3}=2x^{3}} f^{{\prime }}(x)=4*{\frac {1}{2}}x^{3}=2x^{3}
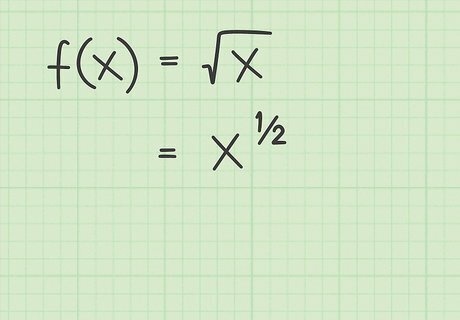
Rewrite the square root as an exponent. To find the derivative of a square root function, you need to remember that the square root of any number or variable can also be written as an exponent. The term below the square root (radical) sign is written as the base, and it is raised to the exponent of 1/2. Consider the following examples: x = x 1 2 {\displaystyle {\sqrt {x}}=x^{\frac {1}{2}}} {\sqrt {x}}=x^{{{\frac {1}{2}}}} 4 = 4 1 2 {\displaystyle {\sqrt {4}}=4^{\frac {1}{2}}} {\sqrt {4}}=4^{{{\frac {1}{2}}}} 3 x = ( 3 x ) 1 2 {\displaystyle {\sqrt {3x}}=(3x)^{\frac {1}{2}}} {\sqrt {3x}}=(3x)^{{{\frac {1}{2}}}} Remember that square roots are the opposite of squaring because roots and exponents are opposites. For example, the four squared is 16. Therefore, the square root of 16 is four. So, if you are trying to get the square root of some number, see if the number is a perfect square. For example, if you have to find the square root of 81. Think whether you can multiply a number by itself to get 81. You know that nine times nine is 81. So nine squared is 81. That means the square root of 81 is nine. There are so many numbers that you could be guessing with this method. You can try out seven and eight. If it is too small, you can go up to nine. If you try out 10, 10 squared is 100. That is too large. You might have to go smaller.
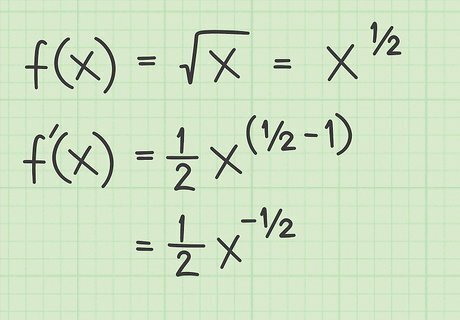
Apply the power rule. If the function is the simplest square root, f ( x ) = x {\displaystyle f(x)={\sqrt {x}}} f(x)={\sqrt {x}}, apply the power rule as follows to find the derivative: f ( x ) = x {\displaystyle f(x)={\sqrt {x}}\ \ \ \ \ } f(x)={\sqrt {x}}\ \ \ \ \ (Write the original function.) f ( x ) = x ( 1 2 ) {\displaystyle f(x)=x^{({\frac {1}{2}})}\ \ \ \ \ } f(x)=x^{{({\frac {1}{2}})}}\ \ \ \ \ (Rewrite the radical as an exponent.) f ′ ( x ) = 1 2 x ( 1 2 − 1 ) {\displaystyle f^{\prime }(x)={\frac {1}{2}}x^{({\frac {1}{2}}-1)}\ \ \ } f^{{\prime }}(x)={\frac {1}{2}}x^{{({\frac {1}{2}}-1)}}\ \ \ (Find derivative with the power rule.) f ′ ( x ) = 1 2 x ( − 1 2 ) {\displaystyle f^{\prime }(x)={\frac {1}{2}}x^{(-{\frac {1}{2}})}\ \ \ } f^{{\prime }}(x)={\frac {1}{2}}x^{{(-{\frac {1}{2}})}}\ \ \ (Simplify exponent.)
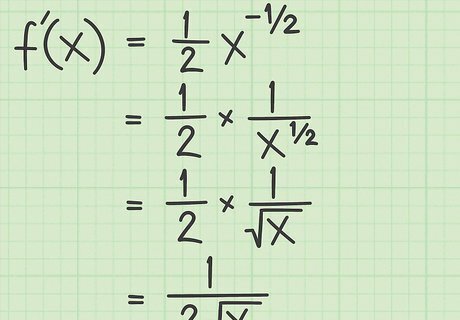
Simplify the result. At this stage, you need to recognize that a negative exponent means to take the reciprocal of what the number would be with the positive exponent. The exponent of − 1 2 {\displaystyle -{\frac {1}{2}}} -{\frac {1}{2}} means that you will have the square root of the base as the denominator of a fraction. Continuing with the square root of x function from above, the derivative can be simplified as: f ′ ( x ) = 1 2 x − 1 2 {\displaystyle f^{\prime }(x)={\frac {1}{2}}x^{-{\frac {1}{2}}}} f^{{\prime }}(x)={\frac {1}{2}}x^{{-{\frac {1}{2}}}} f ′ ( x ) = 1 2 ∗ 1 x {\displaystyle f^{\prime }(x)={\frac {1}{2}}*{\frac {1}{\sqrt {x}}}} f^{{\prime }}(x)={\frac {1}{2}}*{\frac {1}{{\sqrt {x}}}} f ′ ( x ) = 1 2 x {\displaystyle f^{\prime }(x)={\frac {1}{2{\sqrt {x}}}}} f^{{\prime }}(x)={\frac {1}{2{\sqrt {x}}}}
Using the Chain Rule for Square Root Functions
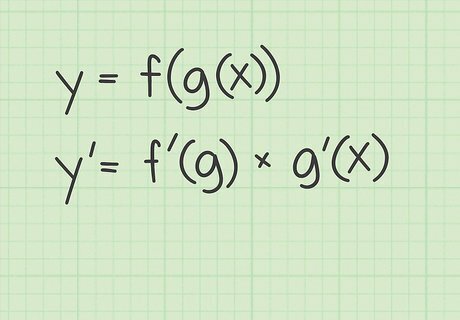
Review the chain rule for functions. The chain rule is a rule for derivatives that you use when the original function combines a function within another function. The chain rule says that, for two functions f ( x ) {\displaystyle f(x)} f(x) and g ( x ) {\displaystyle g(x)} g(x), the derivative of the combination of the two can be found as follows: If y = f ( g ( x ) ) {\displaystyle y=f(g(x))} y=f(g(x)), then y ′ = f ′ ( g ) ∗ g ′ ( x ) {\displaystyle y^{\prime }=f^{\prime }(g)*g^{\prime }(x)} y^{{\prime }}=f^{{\prime }}(g)*g^{{\prime }}(x).
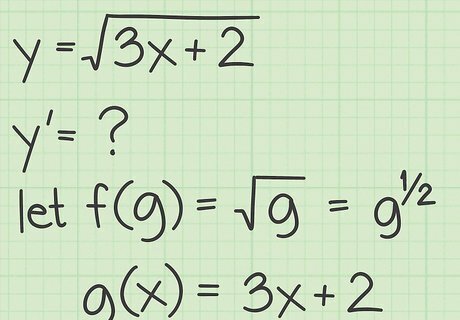
Define the functions for the chain rule. Using the chain rule requires that you first define the two functions that make up your combined function. For square root functions, the outer function f ( g ) {\displaystyle f(g)} f(g) will be the square root function, and the inner function g ( x ) {\displaystyle g(x)} g(x) will be whatever appears under the radical sign. For example, suppose you wish to find the derivative of 3 x + 2 {\displaystyle {\sqrt {3x+2}}} {\sqrt {3x+2}}. Define the two parts as follows: f ( g ) = g = g 1 2 {\displaystyle f(g)={\sqrt {g}}=g^{\frac {1}{2}}} f(g)={\sqrt {g}}=g^{{{\frac {1}{2}}}} g ( x ) = ( 3 x + 2 ) {\displaystyle g(x)=(3x+2)} g(x)=(3x+2)
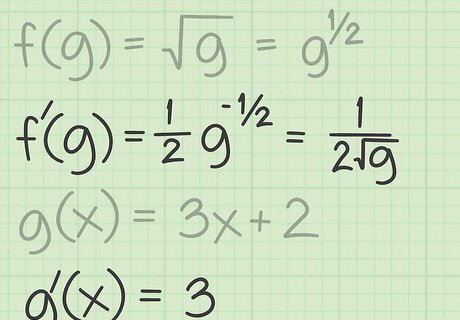
Find the derivatives of the two functions. To apply the chain rule to the square root of a function, you will first need to find the derivative of the general square root function: f ( g ) = g = g 1 2 {\displaystyle f(g)={\sqrt {g}}=g^{\frac {1}{2}}} f(g)={\sqrt {g}}=g^{{{\frac {1}{2}}}} f ′ ( g ) = 1 2 g − 1 2 {\displaystyle f^{\prime }(g)={\frac {1}{2}}g^{-{\frac {1}{2}}}} f^{{\prime }}(g)={\frac {1}{2}}g^{{-{\frac {1}{2}}}} f ′ ( g ) = 1 2 g {\displaystyle f^{\prime }(g)={\frac {1}{2{\sqrt {g}}}}} f^{{\prime }}(g)={\frac {1}{2{\sqrt {g}}}} Then find the derivative of the second function: g ( x ) = ( 3 x + 2 ) {\displaystyle g(x)=(3x+2)} g(x)=(3x+2) g ′ ( x ) = 3 {\displaystyle g^{\prime }(x)=3} g^{{\prime }}(x)=3
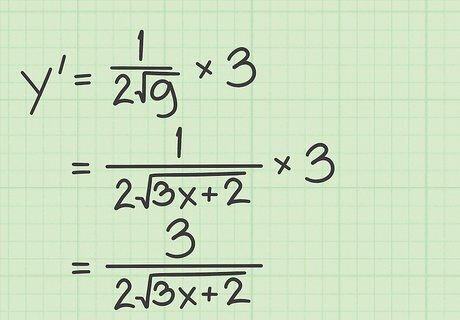
Combine the functions in the chain rule. Recall the chain rule, y ′ = f ′ ( g ) ∗ g ′ ( x ) {\displaystyle y^{\prime }=f^{\prime }(g)*g^{\prime }(x)} y^{{\prime }}=f^{{\prime }}(g)*g^{{\prime }}(x), and then combine the derivatives as follows: y ′ = 1 2 g ∗ 3 {\displaystyle y^{\prime }={\frac {1}{2{\sqrt {g}}}}*3} y^{{\prime }}={\frac {1}{2{\sqrt {g}}}}*3 y ′ = 1 2 ( 3 x + 2 ∗ 3 {\displaystyle y^{\prime }={\frac {1}{2{\sqrt {(3x+2}}}}*3} y^{{\prime }}={\frac {1}{2{\sqrt {(3x+2}}}}*3 y ′ = 3 2 ( 3 x + 2 {\displaystyle y^{\prime }={\frac {3}{2{\sqrt {(3x+2}}}}} y^{{\prime }}={\frac {3}{2{\sqrt {(3x+2}}}}
Using a Shortcut for Derivatives of Radical Functions
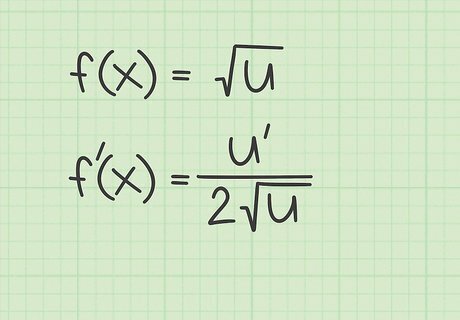
Learn the shortcut for derivatives of any radical function. Whenever you wish to find the derivative of the square root of a variable or a function, you can apply a simple pattern. The derivative will always be the derivative of the radicand, divided by double the original square root. Symbolically, this can be shown as: If f ( x ) = u {\displaystyle f(x)={\sqrt {u}}} f(x)={\sqrt {u}}, then f ′ ( x ) = u ′ 2 u {\displaystyle f^{\prime }(x)={\frac {u^{\prime }}{2{\sqrt {u}}}}} f^{{\prime }}(x)={\frac {u^{{\prime }}}{2{\sqrt {u}}}}
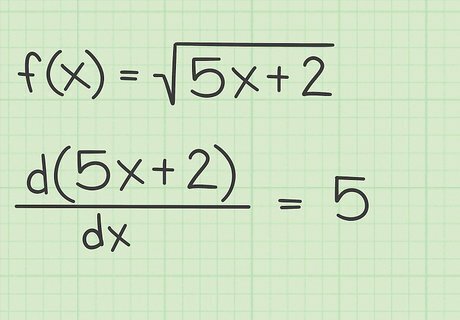
Find the derivative of the radicand. The radicand is the term or function underneath the square root sign. To apply this shortcut, find the derivative of the radicand alone. Consider the following examples: In the function 5 x + 2 {\displaystyle {\sqrt {5x+2}}} {\sqrt {5x+2}}, the radicand is ( 5 x + 2 ) {\displaystyle (5x+2)} (5x+2). Its derivative is 5 {\displaystyle 5} 5. In the function 3 x 4 {\displaystyle {\sqrt {3x^{4}}}} {\sqrt {3x^{4}}}, the radicand is 3 x 4 {\displaystyle 3x^{4}} 3x^{4}. Its derivative is 12 x 3 {\displaystyle 12x^{3}} 12x^{3}. In the function s i n ( x ) {\displaystyle {\sqrt {sin(x)}}} {\sqrt {sin(x)}}, the radicand is sin ( x ) {\displaystyle \sin(x)} \sin(x). Its derivative is cos ( x ) {\displaystyle \cos(x)} \cos(x).
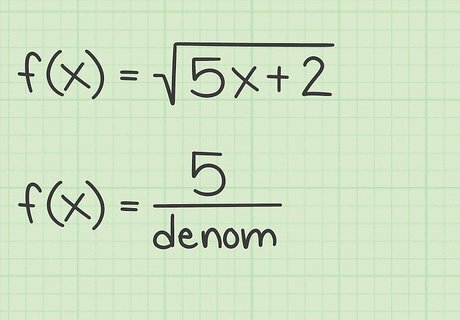
Write the derivative of the radicand as the numerator of a fraction. The derivative of a radical function will involve a fraction. The numerator of this fraction is the derivative of the radicand. Thus, for the sample functions above, the first part of the derivative will be as follows: If f ( x ) = 5 x + 2 {\displaystyle f(x)={\sqrt {5x+2}}} f(x)={\sqrt {5x+2}}, then f ′ ( x ) = 5 denom {\displaystyle f^{\prime }(x)={\frac {5}{\text{denom}}}} f^{{\prime }}(x)={\frac {5}{{\text{denom}}}} If f ( x ) = 3 x 4 {\displaystyle f(x)={\sqrt {3x^{4}}}} f(x)={\sqrt {3x^{4}}}, then f ′ ( x ) = 12 x 3 denom {\displaystyle f^{\prime }(x)={\frac {12x^{3}}{\text{denom}}}} f^{{\prime }}(x)={\frac {12x^{3}}{{\text{denom}}}} If f ( x ) = sin ( x ) {\displaystyle f(x)={\sqrt {\sin(x)}}} f(x)={\sqrt {\sin(x)}}, then f ′ ( x ) = cos ( x ) denom {\displaystyle f^{\prime }(x)={\frac {\cos(x)}{\text{denom}}}} f^{{\prime }}(x)={\frac {\cos(x)}{{\text{denom}}}}
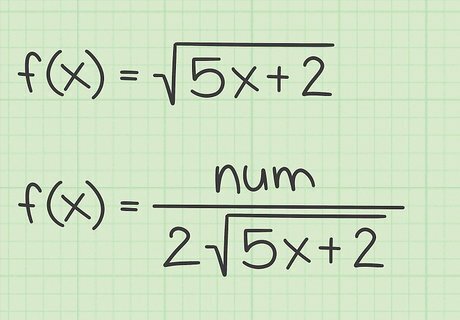
Write the denominator as double the original square root. Using this shortcut, the denominator will be two times the original square root function. Thus, for the three sample functions above, the denominators of the derivatives will be: For f ( x ) = 5 x + 2 {\displaystyle f(x)={\sqrt {5x+2}}} f(x)={\sqrt {5x+2}}, then f ′ ( x ) = num 2 5 x + 2 {\displaystyle f^{\prime }(x)={\frac {\text{num}}{2{\sqrt {5x+2}}}}} f^{{\prime }}(x)={\frac {{\text{num}}}{2{\sqrt {5x+2}}}} If f ( x ) = 3 x 4 {\displaystyle f(x)={\sqrt {3x^{4}}}} f(x)={\sqrt {3x^{4}}}, then f ′ ( x ) = num 2 3 x 4 {\displaystyle f^{\prime }(x)={\frac {\text{num}}{2{\sqrt {3x^{4}}}}}} f^{{\prime }}(x)={\frac {{\text{num}}}{2{\sqrt {3x^{4}}}}} If f ( x ) = sin ( x ) {\displaystyle f(x)={\sqrt {\sin(x)}}} f(x)={\sqrt {\sin(x)}}, then f ′ ( x ) = num 2 sin ( x ) {\displaystyle f^{\prime }(x)={\frac {\text{num}}{2{\sqrt {\sin(x)}}}}} f^{{\prime }}(x)={\frac {{\text{num}}}{2{\sqrt {\sin(x)}}}}
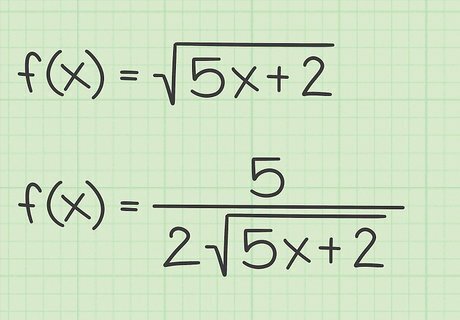
Combine numerator and denominator to find the derivative. Put the two halves of the fraction together, and the result will be the derivative of the original function. For f ( x ) = 5 x + 2 {\displaystyle f(x)={\sqrt {5x+2}}} f(x)={\sqrt {5x+2}}, then f ′ ( x ) = 5 2 5 x + 2 {\displaystyle f^{\prime }(x)={\frac {5}{2{\sqrt {5x+2}}}}} f^{{\prime }}(x)={\frac {5}{2{\sqrt {5x+2}}}} If f ( x ) = 3 x 4 {\displaystyle f(x)={\sqrt {3x^{4}}}} f(x)={\sqrt {3x^{4}}}, then f ′ ( x ) = 12 x 3 2 3 x 4 {\displaystyle f^{\prime }(x)={\frac {12x^{3}}{2{\sqrt {3x^{4}}}}}} f^{{\prime }}(x)={\frac {12x^{3}}{2{\sqrt {3x^{4}}}}} If f ( x ) = sin ( x ) {\displaystyle f(x)={\sqrt {\sin(x)}}} f(x)={\sqrt {\sin(x)}}, then f ′ ( x ) = cos ( x ) 2 sin ( x ) {\displaystyle f^{\prime }(x)={\frac {\cos(x)}{2{\sqrt {\sin(x)}}}}} f^{{\prime }}(x)={\frac {\cos(x)}{2{\sqrt {\sin(x)}}}}

















Comments
0 comment