
views
Flux Through a Surface of Area A

Know the formula for electric flux. The Electric Flux through a surface A is equal to the dot product of the electric field and area vectors E and A. The dot product of two vectors is equal to the product of their respective magnitudes multiplied by the cosine of the angle between them.

Determine the magnitude and direction of your electric field vector. In most cases of this type, it is already given in the problem.
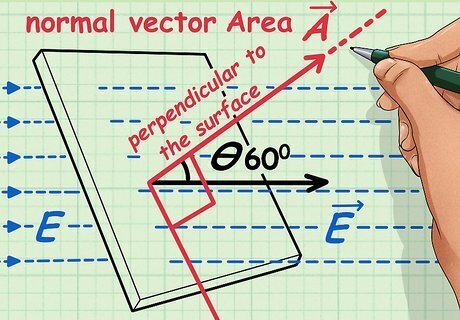
Determine the magnitude and direction of the surface area vector A. Note that the surface area vector is always perpendicular and outward from the surface.
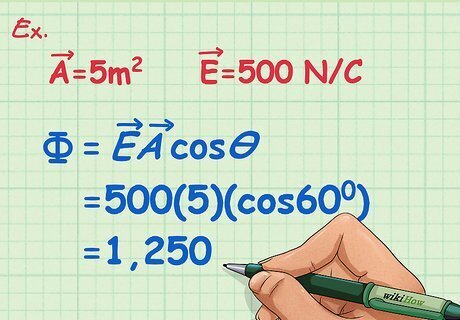
Multiply the magnitude of your surface area vector by the magnitude of your electric field vector and the cosine of the angle between them. The cosine of the angle between the two vectors multiplied by the electric field vector is equal to the component of electric field that is perpendicular to the surface area vector.

Include the proper units. Electric flux is the product of Newtons per Coulomb (E) and meters squared. Proper units for electric flux are Newtons meters squared per coulomb.
Flux Through an Enclosed Surface with Charge q using E field and Surface Area

Know the formula for the electric flux through a closed surface. Net electric flux through a closed surface with enclosed charge q is the integral of the dot product between the electric field and the instantaneous surface area vector. The integral of the instantaneous surface area is simply the surface area vector. The electric field at a distance outside a Gaussian surface will be constant at that specific distance.
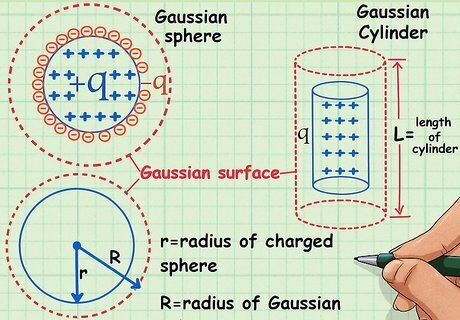
Draw an imaginary Gaussian surface around your charge. Choose one that best fits its dimensions. A solid sphere or spherical shell of charge Q would require the use of a sphere, while a line or rod of charge would require a cylinder. A solid sphere or hollow spherical shell with uniform charge distribution can be treated as if all charge were concentrated at the center (a point charge), therefore the radius of your Gaussian surface would be the radius of your sphere plus the distance away from the sphere's surface.

Determine the surface area of your Gaussian surface. Frequent formulas are 4pi r squared and pi r squared.

Determine the electric field going through your Gaussian surface.
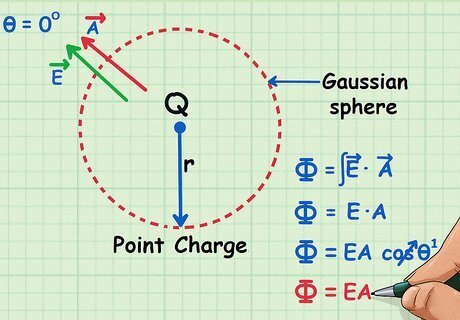
Multiply the magnitude of your surface area vector by the magnitude of your electric field vector and the cosine of the angle between them. With the proper Gaussian surface, the electric field and surface area vectors will nearly always be parallel.

Do not forget to add the proper units for electric flux.
Flux Through an Enclosed Surface with charge q using Q and Epsilon Zero

Know that the dot product of the electric field and area vectors is also equal to the enclosed charge divided by the permittivity constant. The permittivity constant epsilon zero is equal to 8.85E-12.

Find the total charge q enclosed by your Gaussian surface. If given charge density, it is possible to solve for the enclosed charge by multiplying the density by the dimensions of the charge distribution (see above formulas). Note that Q total is the same as the total charge enclosed by your Gaussian surface.
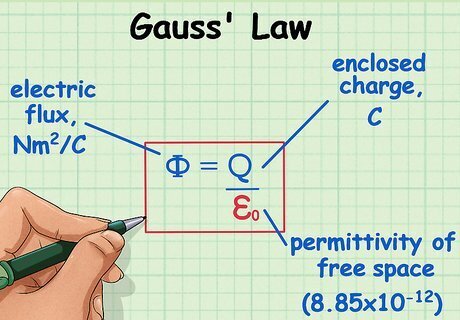
Divide the total enclosed charge by epsilon zero.

Be sure to add the proper units.
















Comments
0 comment