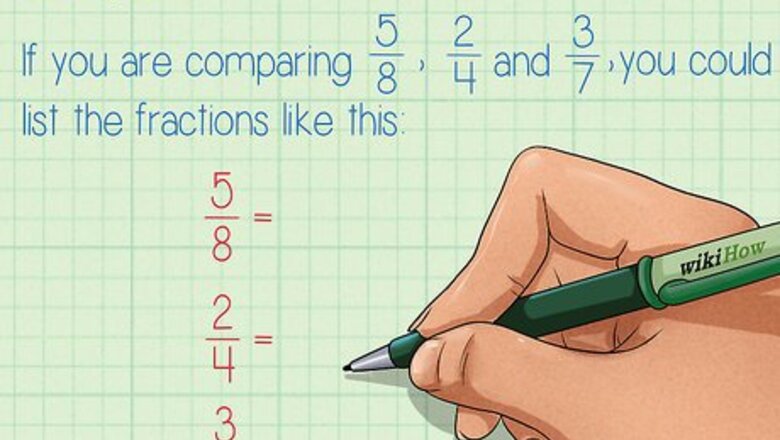
views
3
4
{\displaystyle {\frac {3}{4}}}
of a pizza, or
6
7
{\displaystyle {\frac {6}{7}}}
of a pizza?” There are several ways to compare and order fractions. If you have a calculator, the quickest way is to convert the fractions to decimals. If you don’t have a calculator, you can compare easily by finding common denominators or by simply using your reasoning skills and what you already know about fractions.
Converting Fractions to Decimals
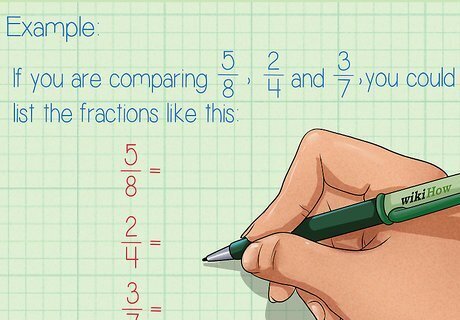
List the fractions you are ordering in one column. Next to each fraction, write an equal sign. It doesn’t matter in what order you list the fractions. For example, if you are comparing 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}, 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}}, and 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}, you could list the fractions like this: 5 8 = {\displaystyle {\frac {5}{8}}=} {\frac {5}{8}}= 2 4 = {\displaystyle {\frac {2}{4}}=} {\frac {2}{4}}= 3 7 = {\displaystyle {\frac {3}{7}}=} {\frac {3}{7}}=
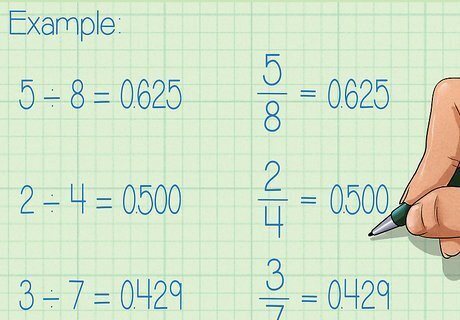
Convert each fraction to a decimal. To do this, divide the numerator of each fraction by its denominator. Place each decimal to the right of its fraction, after the equal sign. The numerator is the number above the fraction bar; the denominator is the number below the fraction bar. You can complete the division using a calculator or by hand using the standard division algorithm. Either way, round to at least two or three decimal places. For example: 5 ÷ 8 = .625 {\displaystyle 5\div 8=.625} 5\div 8=.625, so 5 8 = .625 {\displaystyle {\frac {5}{8}}=.625} {\frac {5}{8}}=.625 2 ÷ 4 = .500 {\displaystyle 2\div 4=.500} 2\div 4=.500, so 2 4 = .500 {\displaystyle {\frac {2}{4}}=.500} {\frac {2}{4}}=.500 3 ÷ 7 = .429 {\displaystyle 3\div 7=.429} 3\div 7=.429, so 3 7 = .429 {\displaystyle {\frac {3}{7}}=.429} {\frac {3}{7}}=.429.
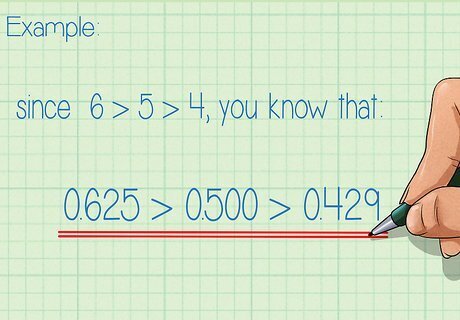
Compare and order the decimals, beginning with the tenths place. The tenths place is the first number to the right of the decimal point. The bigger the number in the tenths place, the bigger the decimal. For example, since 6 > 5 > 4 {\displaystyle 6>5>4} 6>5>4, you know that .625 > .500 > .429 {\displaystyle .625>.500>.429} .625>.500>.429. If all the numbers in the tenths place are the same, then compare the numbers in the hundredths place (the second number to the right of the decimal point).
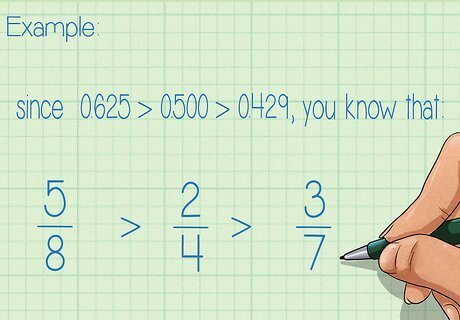
Compare and order the fractions, depending on the order of their corresponding decimals. The order of the fractions will be the same as the order of the decimals, since fractions and decimals are different ways to express the same value. For example, since .625 > .500 > .429 {\displaystyle .625>.500>.429} .625>.500>.429, you know that 5 8 > 2 4 > 3 7 {\displaystyle {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}} {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}.
Finding a Common Denominator
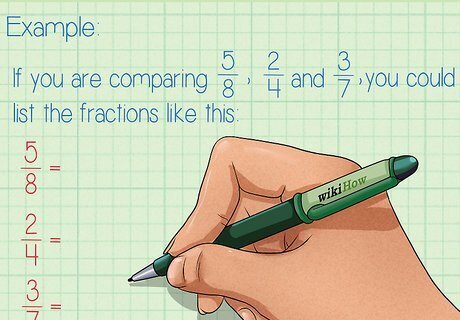
List the fractions you are ordering in one column. To the right of each fraction, draw a blank fraction bar (a bar without any numbers above or below). It doesn’t matter what order you list the fractions. If you have any mixed fractions, you will need to convert them to improper fractions before comparing and ordering. A mixed fraction is a fraction that contains a whole number and a fraction. For instructions on how to do this, read Change Mixed Numbers to Improper Fractions. For example, if you are comparing 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}, 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}}, and 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}, you could list the fractions like this: 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}

Multiply the three denominators together. This will be your new denominator for all three fractions, so place this product underneath all three blank fraction bars. You can complete the multiplication by using a calculator or by using the standard multiplication algorithm. For example, if you are comparing and 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}, 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}}, and 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}, you would calculate 8 × 4 × 7 = 224 {\displaystyle 8\times 4\times 7=224} 8\times 4\times 7=224. Your fractions will then be listed like this: 5 8 x 224 {\displaystyle {\frac {5}{8}}\;{\frac {x}{224}}} {\frac {5}{8}}\;{\frac {x}{224}} 2 4 x 224 {\displaystyle {\frac {2}{4}}\;{\frac {x}{224}}} {\frac {2}{4}}\;{\frac {x}{224}} 3 7 x 224 {\displaystyle {\frac {3}{7}}\;{\frac {x}{224}}} {\frac {3}{7}}\;{\frac {x}{224}}
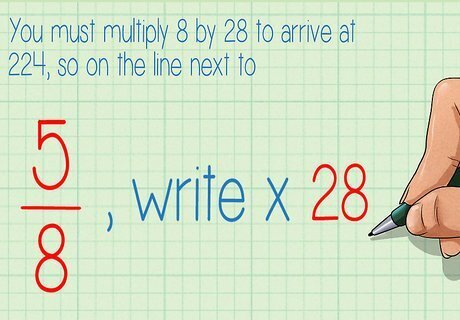
Determine what factor you needed to multiply each original denominator by to arrive at the new denominator. To figure this out, divide the new denominator by the original denominator. Draw a line from each original denominator to each new denominator. Write the missing factor on the line. For example:You must multiply 8 by 28 to arrive at 224, so on the line next to 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}, write × 28 {\displaystyle \times 28} \times 28. You must multiply 4 by 56 to arrive at 224, so on the line next to 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}}, write × 56 {\displaystyle \times 56} \times 56. You must multiply 7 by 32 to arrive at 224, so on the line next to 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}, write × 32 {\displaystyle \times 32} \times 32.
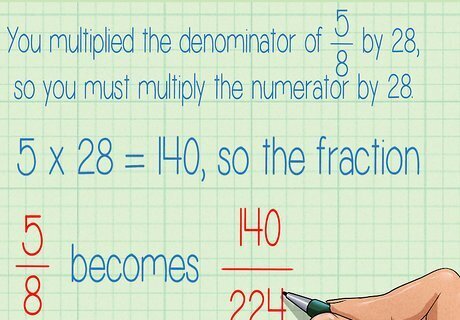
Calculate the new numerator for each fraction. To do this, multiply each original numerator by the same factor you multiplied its denominator by. Fill in the new numerators above the fraction bars. For example:You multiplied the denominator of 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} by 28, so you must multiply the numerator by 28. 5 × 28 = 140 {\displaystyle 5\times 28=140} 5\times 28=140, so the fraction 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} becomes 140 224 {\displaystyle {\frac {140}{224}}} {\frac {140}{224}}. You multiplied the denominator of 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} by 56, so you must multiply the numerator by 56. 2 × 56 = 112 {\displaystyle 2\times 56=112} 2\times 56=112, so the fraction 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} becomes 112 224 {\displaystyle {\frac {112}{224}}} {\frac {112}{224}}.You multiplied the denominator of 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}} by 32, so you must multiply the numerator by 32. 3 × 32 = 96 {\displaystyle 3\times 32=96} 3\times 32=96, so the fraction 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}} becomes 96 224 {\displaystyle {\frac {96}{224}}} {\frac {96}{224}}.

Order the fractions by the size of their new numerators. The larger the numerator, the larger the fraction. You can now order them this way because you found a common denominator and are working with same-sized pieces. For example, to compare 140 224 {\displaystyle {\frac {140}{224}}} {\frac {140}{224}}, 112 224 {\displaystyle {\frac {112}{224}}} {\frac {112}{224}}, and 96 224 {\displaystyle {\frac {96}{224}}} {\frac {96}{224}}, look at their numerators.Since, 140 > 112 > 96 , {\displaystyle 140>112>96,} 140>112>96, you know that 140 224 > 112 224 > 96 224 {\displaystyle {\frac {140}{224}}>{\frac {112}{224}}>{\frac {96}{224}}} {\frac {140}{224}}>{\frac {112}{224}}>{\frac {96}{224}}. If you reduce the fractions, your final answer will be 5 8 > 2 4 > 3 7 {\displaystyle {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}} {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}.
Reasoning About Fraction Size

Compare and order unit fractions. Unit fractions are fractions that have 1 as the numerator. The bigger the denominator is in a unit fraction, the smaller the fraction is. The numerator is the number above the fraction bar. It tells you how many pieces you have. The denominator is the number below the fraction bar. It tells you how many pieces the whole is divided into. The more pieces the whole is divided into, the smaller one piece is. For example, to compare 1 4 {\displaystyle {\frac {1}{4}}} {\frac {1}{4}}, 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}} and 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}}, look at the denominators, 4, 3, and 6. Since 6 > 4 > 3 {\displaystyle 6>4>3} 6>4>3, 1 3 > 1 4 > 1 6 {\displaystyle {\frac {1}{3}}>{\frac {1}{4}}>{\frac {1}{6}}} {\frac {1}{3}}>{\frac {1}{4}}>{\frac {1}{6}}.

Compare and order fractions with the same denominator. Because these fractions have the same denominator, that means you are working with same-sized pieces of a whole. All you need to do then is compare how many pieces you have, which is given in the numerator. For example, to compare 1 6 {\displaystyle {\frac {1}{6}}} {\frac {1}{6}}, 5 6 {\displaystyle {\frac {5}{6}}} {\frac {5}{6}}, and 3 6 {\displaystyle {\frac {3}{6}}} {\frac {3}{6}}, look at the numerators, 1, 5, and 3. You have one piece, five pieces, and 3 pieces. Since 5 > 3 > 1 {\displaystyle 5>3>1} 5>3>1, 5 6 > 3 6 > 1 6 {\displaystyle {\frac {5}{6}}>{\frac {3}{6}}>{\frac {1}{6}}} {\frac {5}{6}}>{\frac {3}{6}}>{\frac {1}{6}}.

Compare and order fractions with the same numerator. Remember, the bigger the denominator, the more pieces the whole is divided into, and therefore the smaller each piece will be. So if you have the same number of pieces, by comparing the size of the pieces, you should be able to compare and order. For example, to compare 4 7 {\displaystyle {\frac {4}{7}}} {\frac {4}{7}}, 4 5 {\displaystyle {\frac {4}{5}}} {\frac {4}{5}}, and 4 9 {\displaystyle {\frac {4}{9}}} {\frac {4}{9}}, look at the denominators, 7, 5, and 9. A whole cut into 9 pieces has smaller pieces than a whole cut into 7 pieces, and a whole cut into 7 pieces has smaller pieces than a whole cut into 5 pieces. So 4 5 > 4 7 > 4 9 {\displaystyle {\frac {4}{5}}>{\frac {4}{7}}>{\frac {4}{9}}} {\frac {4}{5}}>{\frac {4}{7}}>{\frac {4}{9}}.

Use benchmark fractions. A benchmark fractions is one you can easily visualize, such as 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. By comparing the fractions you are working with to a benchmark fraction, you may be able to use reasoning to determine their order. For example, to compare 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}}, 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}}, and 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}}, compare all of these fractions to 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}. You should see that 5 8 {\displaystyle {\frac {5}{8}}} {\frac {5}{8}} is a little more than 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}, because 4 8 = 1 2 {\displaystyle {\frac {4}{8}}={\frac {1}{2}}} {\frac {4}{8}}={\frac {1}{2}}. On the other hand, 3 7 {\displaystyle {\frac {3}{7}}} {\frac {3}{7}} is a little less than 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}}, because 3 is less than half of 7. (3.5 is half of seven.) 2 4 {\displaystyle {\frac {2}{4}}} {\frac {2}{4}} is exactly equal to 1 2 {\displaystyle {\frac {1}{2}}} {\frac {1}{2}} So, you can reason that 5 8 > 2 4 > 3 7 {\displaystyle {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}} {\frac {5}{8}}>{\frac {2}{4}}>{\frac {3}{7}}.


















Comments
0 comment