
views
Calculating Annual Payments on a Loan

Familiarize yourself with the formula for calculating annual payments on a loan. Assuming a fixed interest rate and evenly spaced payments, the annual payment amount for an annuity (anything that must be paid in yearly increments) can be determined using the following formula: A n n u a l P a y m e n t = ( r ( P ) ) ( 1 − ( 1 + r ) − n ) {\displaystyle AnnualPayment={\frac {(r(P))}{(1-(1+r)^{-n})}}} AnnualPayment={\frac {(r(P))}{(1-(1+r)^{{-n}})}}

Understand the variables in the equation. The first step of finding annual payments on a loan is to understand what each of the letters means. Fortunately, each letter simply represents one of the elements of a loan. This information can be easily found on your loan agreement.If you don't have a copy of your loan agreement, contact your lender. r represents the interest rate per period. Because this represents an annual interest rate in this case, this number may be referred to as an APR (annual percentage rate). P represents the principal, or the amount borrowed. This can also be referred to as the present value. N represents the number of periods in the loan. In this case, periods equals years, and would just be the number of years on your loan agreement.

Plug the values into the formula. Once you know the terms of your loan, you can plug them into the formula above to determine the annual payment. For example, consider a $10,000 loan with an annual interest rate of 9%, for a period of two years. A n n u a l P a y m e n t = ( 0.09 ( $ 10 , 000 ) ) ( 1 − ( 1 + 0.09 ) − 2 ) {\displaystyle AnnualPayment={\frac {(0.09(\$10,000))}{(1-(1+0.09)^{-2})}}} AnnualPayment={\frac {(0.09(\$10,000))}{(1-(1+0.09)^{{-2}})}} Note that when inputting a percent (9% in this case), it must be input as a decimal. 9% therefore becomes .09.

Solve for the numerator of the equation. The first step in calculating annual payments on a loan is to solve for the numerator (the top part of the equation). Multiply .09 x $10,000 to get $900. This completes the left side of the equation. Your equation should now look like this: A n n u a l P a y m e n t = $ 900 ( 1 − ( 1 + 0.09 ) − 2 ) {\displaystyle AnnualPayment={\frac {\$900}{(1-(1+0.09)^{-2})}}} AnnualPayment={\frac {\$900}{(1-(1+0.09)^{{-2}})}}

Solve for the denominator. The next step is to solve the denominator (the bottom part of the equation). This will be done in three steps. First, add 1 to .09, to give 1.09. Your equation should now look like this: A n n u a l P a y m e n t = $ 900 ( 1 − ( 1.09 ) − 2 ) {\displaystyle AnnualPayment={\frac {\$900}{(1-(1.09)^{-2})}}} AnnualPayment={\frac {\$900}{(1-(1.09)^{{-2}})}}

Solve for the exponent. Raise 1.09 to the power of -2 (the term). The result will be 0.8417. Recall that when solving an equation, brackets are always solved first, followed by exponents (the -2). Your equation should now look like this: A n n u a l P a y m e n t = $ 900 1 − ( 0.8417 ) {\displaystyle AnnualPayment={\frac {\$900}{1-(0.8417)}}} AnnualPayment={\frac {\$900}{1-(0.8417)}}

Finish solving for the denominator. Subtract 0.8417 from 1, to obtain 0.1583. This would complete the bottom part of the equation. Remember to keep as many decimal places present in calculation as possible. This will ensure accuracy, especially in larger loan amounts. Your equation should now look like this: A n n u a l P a y m e n t = $ 900 0.1583 {\displaystyle AnnualPayment={\frac {\$900}{0.1583}}} AnnualPayment={\frac {\$900}{0.1583}}

Complete your calculation. Divide the top of your equation by the bottom to get the annual payment on your loan. Solving the example equation, you get 5685.41. Therefore, your annual payment would be $5,685.41.

Use online resources to construct an amortization table to understand the annual payments. An amortization table allows you to see each payment you will make for the remainder of your loan, broken down into how much is principal, how much is interest, and what the remaining balance on the loan is. This allows you to see exactly what your monthly (or annual) payment is, and less and less of the payment goes to interest over time as the amount owed decreases. Simply input the amount, interest rate, and term into the calculator, and the amortization table will show every monthly payment from the current point to the end of the loan.
Calculating Periodic Payments On A Loan

Understand the reason to calculate periodic payments on a loan. Often, lenders require that you make monthly or quarterly payments. Therefore, it is more useful to know what the monthly or quarterly payment is, rather than simply the annual payment. Fortunately, the same formula is used, with some minor revisions. For the sake of this example, assume the new loan is the same as previously-discussed one, with the only change being you are now required to make monthly payments for the two year period.

Learn the formula for calculating periodic payments on a loan. Although the formula is largely the same as that for annual payments, a few minor changes occur to reflect the fact that there are now more payments. Again, the standard formula is: P a y m e n t = ( r ( P ) ) ( 1 − ( 1 + r ) − n ) {\displaystyle Payment={\frac {(r(P))}{(1-(1+r)^{-n})}}} Payment={\frac {(r(P))}{(1-(1+r)^{{-n}})}} First, the amount of periods in the loan, or "n", would change. Instead of being 2 (representing two years before, or two annual payments), it is now 24 for monthly payments (representing 1 payment a month for 2 years) and 8 for quarterly payments (representing one payment each quarter for the two years). Second, the annual interest rate would need to change to reflect the fact there are more payments. To determine an interest rate for periodic payments, divide the annual interest rate by the number of payments required within a year. For example, a 9% annual interest rate is equivalent to a .0075 or .75% monthly interest rate (.09/12).

Fill in the equation with your values. The new formula, with all the example numbers plugged in looks like this: P a y m e n t = ( 0.09 12 ( $ 10 , 000 ) ) ( 1 − ( 1 + 0.09 12 ) − 24 ) {\displaystyle Payment={\frac {({\frac {0.09}{12}}(\$10,000))}{(1-(1+{\frac {0.09}{12}})^{-24})}}} Payment={\frac {({\frac {0.09}{12}}(\$10,000))}{(1-(1+{\frac {0.09}{12}})^{{-24}})}}
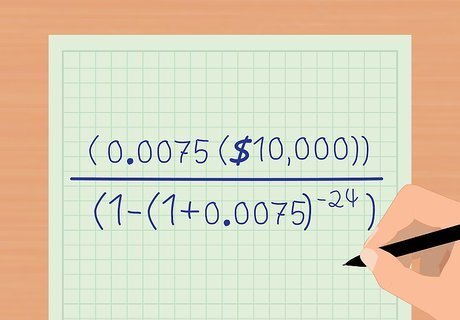
Begin to calculate the periodic payments on the loan. Start by simplifying the rate by solving for the monthly interest rate. This is done by dividing the annual rate of 9% by 12, as in the equation, to get 0.0075. After you do so, your equation should look like this: P a y m e n t = ( 0.0075 ( $ 10 , 000 ) ) ( 1 − ( 1 + 0.0075 ) − 24 ) {\displaystyle Payment={\frac {(0.0075(\$10,000))}{(1-(1+0.0075)^{-24})}}} Payment={\frac {(0.0075(\$10,000))}{(1-(1+0.0075)^{{-24}})}}

Solve the numerator. Continue by solving the numerator (the top part of the equation). Multiply the two numbers (rate and principal) together to solve this step. Your equation should now look like this: P a y m e n t = ( $ 75 ) ( 1 − ( 1 + 0.0075 ) − 24 ) {\displaystyle Payment={\frac {(\$75)}{(1-(1+0.0075)^{-24})}}} Payment={\frac {(\$75)}{(1-(1+0.0075)^{{-24}})}}

Simplify the denominator. Next, simplify the denominator (bottom of the equation) by adding the rate to 1. This comes to 1.0075 in our example. The equation now looks like this: P a y m e n t = ( $ 75 ) ( 1 − ( 1.0075 ) − 24 ) {\displaystyle Payment={\frac {(\$75)}{(1-(1.0075)^{-24})}}} Payment={\frac {(\$75)}{(1-(1.0075)^{{-24}})}}
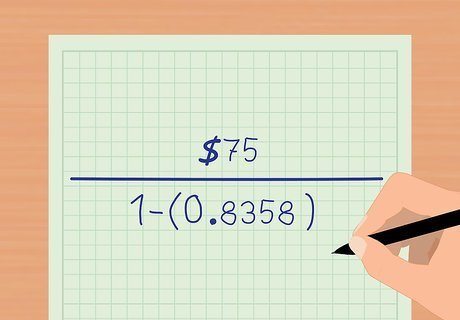
Solve the exponent. Next, solve the exponent in the equation by raising the (rate +1) found in the last step to the power of -24. This comes to 0.8358. The equation now looks like this: P a y m e n t = $ 75 1 − ( 0.8358 ) {\displaystyle Payment={\frac {\$75}{1-(0.8358)}}} Payment={\frac {\$75}{1-(0.8358)}}
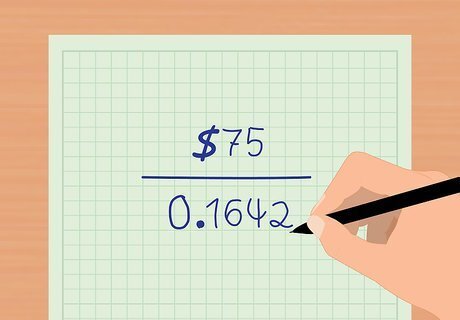
Simplify the denominator again. Simplify by subtracting your result in the last step from one. In our example, this would be 1 − 0.8358 {\displaystyle 1-0.8358} 1-0.8358, which yields 0.1642. At this point, the equation looks like this: P a y m e n t = $ 75 0.1642 {\displaystyle Payment={\frac {\$75}{0.1642}}} Payment={\frac {\$75}{0.1642}}

Solve for your monthly payment. Finally, divide the top part of the equation by the bottom to get your monthly payment. In this case, P a y m e n t = $ 456.76 {\displaystyle Payment=\$456.76} Payment=\$456.76
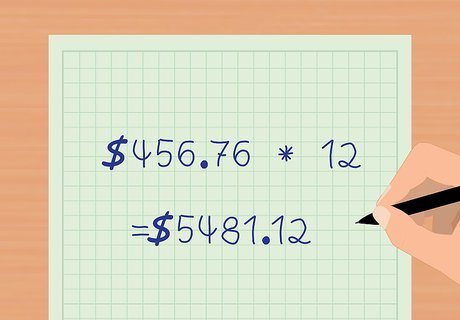
Convert your answer to an annual payment total. If necessary, you can convert your monthly payment to an annual total by multiplying it by 12. Here, 12 ∗ 473.78 = $ 5 , 481.12 {\displaystyle 12*473.78=\$5,481.12} 12*473.78=\$5,481.12.
Use an online calculator to confirm results. Once again, keep in mind that there are plenty of online calculators available to calculate this online, without ever calculating the payment yourself.



















Comments
0 comment